鲁大荒 @AISERLU
#MIDJOURNEY #CHATGPT #AIGC
完美曲线是一个在不同领域和语境中有不同含义的概念,无论是严格的几何定义,还是自然界的曲线美,或者是艺术创作中的自由表达,完美曲线都承载了和谐、平衡、流动和美感等共同特质。完美曲线是一个高度主观且多维的概念,它在不同语境中代表了不同的标准和美学。完美曲线不仅是数学、自然科学和艺术领域的研究对象,更是算法实现的核心内容。完美曲线不仅在各自的领域中具有重要意义,而且其算法实现方式也反映了人类对自然和艺术美感的深刻理解。随着计算能力的提升和算法的发展,我们能够更精确地模拟和创造这些曲线,推动相关领域的发展。
审美的终极形式:理性与普遍性
康德在《判断力批判》中提出,审美判断不仅是主观的感官愉悦,更是理性的一种活动。他认为,审美判断具有“普遍性”,即尽管审美体验是主观的,但人们在审美判断中寻求一种普遍的共识,这种共识超越了个人的偏好,指向一种理性的标准。
在康德看来,审美的终极形式并非感官的多样性,而是理性对美的普遍性判断。这种判断不仅仅是对感官的满足,更是对人类理性的一种体现。
完美曲线的审美标准
如果我们将完美曲线视为审美的一个重要方面,那么它的“完美”不仅仅是感官上的愉悦,更是理性上的和谐。例如,圆形以其无限的对称性和均衡感,被视为几何学中的理想形状。这种理想性不仅仅是感官上的享受,更是理性对和谐与秩序的追求,它超越了个人的感官体验,指向一种普遍的审美理性(Common Sense)。
审美的终极形式绝对不是无限的,尤其是在完美曲线的语境下,亦并非感官的多样性,而是理性对美的普遍性判断。这种判断超越了个人的偏好,指向一种普遍的审美标准。
完美曲线的理性与普遍性法则
在形而上的终极视野里,“完美曲线”并不是一个任意伸展的无穷集合,而是若干可被理性压缩成原型的有限范畴。从哲学对“普遍性”的要求、到数学对“同构”的归类,再到自然与工程实践的审美检验,最终只剩下四大原型:圆、等角螺旋、单调曲率美学曲线、以及自相似分形边界。它们分别对应“绝对对称”“比例生长”“平滑和谐”“完美复杂”四条普遍美学法则。其它所有赏心悦目的曲线,要么在同构意义上可归入这四类,要么只是它们的组合、截取或变形。
1 理性为何把无限曲线压缩成有限 archetypes
1.1 哲学公设:审美要能“可普遍传递”
- 康德指出,美感判断若要具有“趋向普遍性”,就必须诉诸一种先天的共同感 (sensus communis) — 既是主观快感,又可理性沟通 (哲学百科全书, 斯坦福哲学百科全书)。
- 柏拉图在《蒂迈欧》中把“圆”奉为世界秩序的原型;形而上之“形相”只有少数,感官之“多样”不过是模仿 (斯坦福哲学百科全书, Wikipedia)。
1.2 数学公设:同构分类让“形”归一
- 解析几何把平面曲线按对称群与常曲率条件分成有限族;Lie-群分类给出等价类只有少数基本模式 (科学直通车)。
- 代数几何用双有理 (birational) 等价把无穷多条代数曲线化简为按“属(genus)”分层的离散簇 (Wikipedia, 加州大学伯克利分校数学系)。
- 罗素早就指出,纯数学一切对象可归约为少数逻辑范畴 (马萨诸塞大学网站)。
2 四大“终极完美曲线”原型
我们不妨借用“原型分析”的方式,归纳总结视觉与认知上的四种基本审美角色原型——它们各自主宰了一种秩序,一种思维方式,一种自然或人造世界的极致构型。
圆(Circle)|“永恒者”原型
- 原型身份:宇宙之眼、轮回之环、神圣边界
- 几何神性:唯一全向对称形,0到360度无始无终
- 心理象征:包容、静默、统一、永恒 —— 禅宗中的「円相」本质上是对“空”与“无我”的图形化
- 现实映射:星体轨道、古币、建筑穹顶、车轮、香炉、眼睛
- 哲学意涵:柏拉图几何宇宙的绝对起点;“天圆地方”的原型世界观
它是完美的终点,也是完美的起点。圆不是线的尽头,而是维度的重生。
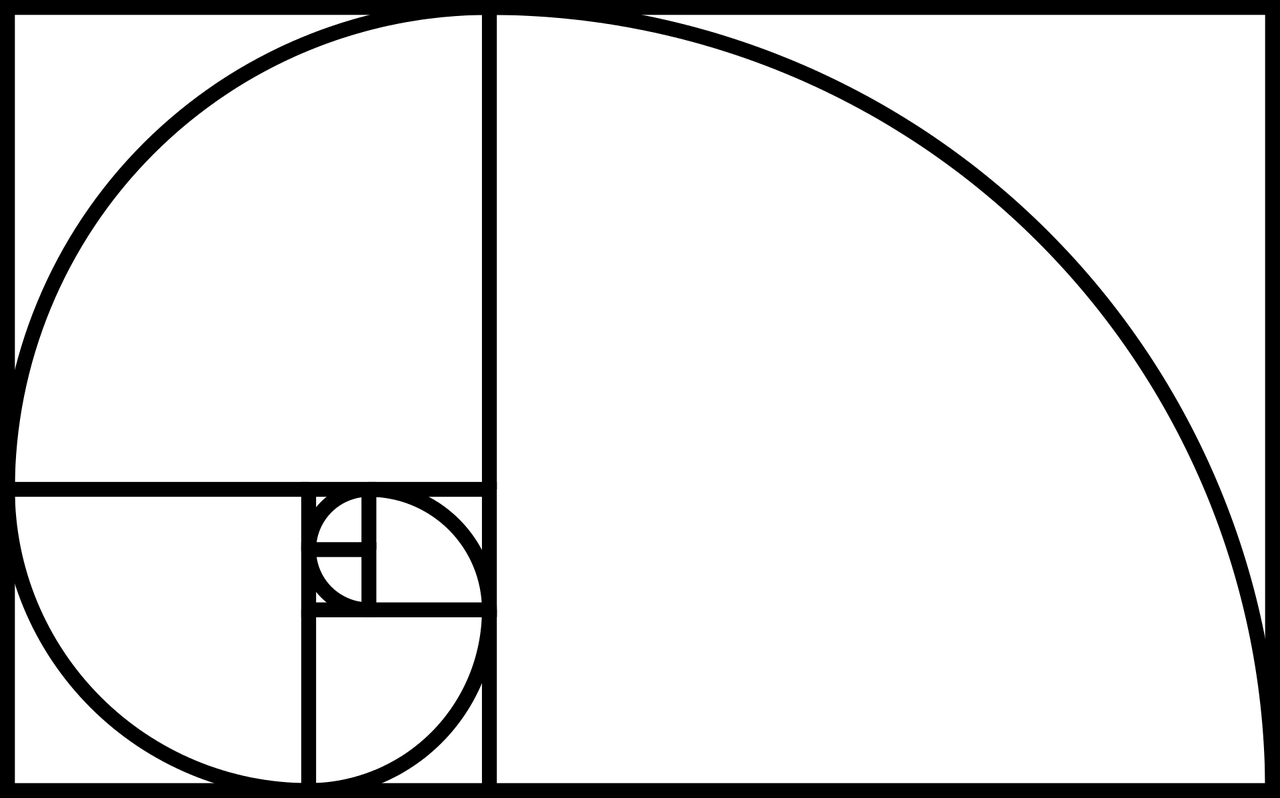
等角螺旋(Logarithmic Spiral)|“生长者”原型
- 原型身份:自然的密码、永续的涌动者
- 几何神性:恒定角度的生长,自相似但永不重合
- 心理象征:时间、进化、内在节律、成长中的秩序感
- 现实映射:鹦鹉螺壳、银河系、飓风、花序、DNA
- 哲学意涵:一切生命体的结构默契,黄金比例是美的递归逻辑
它不是静态的图形,而是时间本身的优雅草图。
单调曲率曲线(Log-aesthetic/Superspiral)|“设计者”原型
- 原型身份:人类之手的完美控形者
- 几何神性:在连续中追求不突兀的变化 —— 曲率的单调渐变
- 心理象征:光滑感、速度感、流动中的精致控制
- 现实映射:汽车流线、品牌字体、工业外形、刀刃和机壳
- 哲学意涵:人类智慧对“美”的工程化提炼,现代审美工业的黄金曲线
如果黄金螺旋来自自然,那么log-aesthetic来自意志;这是人为完美的意志性曲线。
分形边界(Fractal Boundary)|“混沌者”原型
- 原型身份:边界行者,秩序之边的缪斯
- 几何神性:在无限复杂中蕴含严格自洽,介于已知与未知之间
- 心理象征:不可穷尽的想象力、神秘、启示、直觉爆炸
- 现实映射:曼德博集、雪花曲线、自然地貌(海岸线、云朵、树枝)、AI生成艺术
- 哲学意涵:宇宙边缘的结构诗,混沌与秩序之间的数学之美
分形不是图形,它是一种世界观:没有中心,也没有尽头;美,在边缘蔓延。

©️Common Sense of Perfect Curves
原型对照表:
| 原型 | 几何精神 | 关键机制 | 审美方向 | 代表意义 |
|---|---|---|---|---|
| 圆 | 全向对称 | 常曲率 | 和谐、静穆 | 统一与永恒的象征 |
| 螺旋 | 自相似 + 恒角度 | 指数增长 | 节奏、生命力 | 自然生长与比例之美 |
| 单调曲率 | 曲率单调变化 | 最平滑设计 | 工业、流动感 | 人工设计中的“自然感” |
| 分形 | 无限复杂/维数>1 | 迭代/分支发散 | 惊奇、混沌美学 | “复杂秩序”哲学原型 |
为什么不是更多?
- 对称群/曲率约束:若要求全向对称→惟有圆;要求螺线对数比例→唯一等角螺旋。
- 曲率单调:满足工业美学“G³-连续”者收敛到 log-aesthetic 家族。
- 自相似:在二维复迭代里,连通且界非平凡的自相似集典型代表就是曼德博集及其子逼近。进一步放宽条件,得到的只是它们的渐近形、裁剪片段或混合拼接,并不产生新的“同构类”。
3 算法生成与可感经验
- 圆与椭圆族可由二次方程一次性绘制;抗 aliasing 的 Bresenham-Midpoint 算法把离散像素逼近几何极限。
- 等角螺旋可用极坐标累乘,也可用离散黄金矩形迭代在像素栅格中逼近。
- 单调曲率曲线需对离散控制点解最小化ds/dk的优化问题——CAD 中已内置商业求解器输出G³‐连续曲线,随后可转成 NURBS 供曲面拼接。
- 曼德博边界的逃逸次数算法在 GPU 上并行迭代即可呈现无限细节;放大再放大,形态始终自相似。
4 基本法则
- 理性层面:四大 archetypes 已足以覆盖“绝对对称—比例生长—平滑和谐—自相似复杂”这四条人类公认的美学法则;它们共同满足康德所谓“没有概念而有普遍性”的审美理性。
- 经验层面:世间无数迷人曲线皆可视为上述四类的衍射与变调。
- 实践层面:算法已能逐一精确生成这四类曲线,为艺术、建筑、工程与新媒体提供“终极曲线字典”。
5 当代应用 —— 让“终极曲线”走出纸面
- 建筑:卡拉特拉瓦的“活体”曲线
西班牙工程师‐建筑师 Santiago Calatrava 几乎把等角螺旋与 G³ 曲线写进钢筋混凝土:密尔沃基美术馆张翼、曼哈顿 PATH 车站“骨鸟”、Turning Torso 住宅塔均借助高度曲率连续的白色弦线呈现“结构即雕塑”的张力。 - 工业设计:Bézier 曲线从车壳到字体
贝济埃 1960 年代为雷诺车壳创建“Bezier 曲线”——实际上是可调阶 NURBS 的先驱,为现代曲面设计奠基,使设计者得以在 CAD 中直接操控曲率分布。 - 生成艺术:分形-Figurative 混血
艺术家利用遗传算法“进化”曼德博集合,逼近具象人像,证明分形边界可融入高阶语义。
6 哲学与人类知觉更新
- 柏拉图:以圆与五正体诠释宇宙秩序,美即对称与比例。
- 康德:美感是“无概念而合目的”的自由合目的性;圆与螺旋恰好最大化形式‐功能的双向可读性。
- 康定斯基:在《点•线•面》中把线性时间-节奏注入曲线,预示单调曲率曲线的情感张力
认知科学实验证明,G³ 连续和对数螺线在观看者的微眼动模式中触发最少的“修正扫视”,对应“认知流畅”与愉悦的主观评分。

黑格尔谈“理想之美”──曲率与比例的哲学地位
在黑格尔现存的《美学讲座》(Hotho 1835 编订,常被中文译作《论艺术的绝对精神》)中,有若干与“几何比例、理想曲线、完美形式”直接相关的段落。不过他讨论的重点 并不是 数学曲线本身,而是把“理想曲线”当作 “理念(Idee)在感性显现中的自由形态” 来阐释。换言之,黑格尔借希腊雕塑与建筑说明:当外在形体的曲率、比例与内在理念完全合一时,就构成了“绝对精神”在艺术中的自我呈现。下面列出黑格尔最贴近“完美曲线”主题的核心论述、出处与解读方式。
- “美是理念的感性闪现”
黑格尔在导论中反复强调,美(尤其是古典之美)就是理念与感性形态的即刻统一。当形体的 曲率、比例、姿态 不再显得外在偶然,而成为理念自身的自然流露时,我们才称之为“理想”。 - 希腊雕塑的“圆满闭合”
在《雕塑理想》一章,黑格尔用“闭合的、无余的圆形统一”形容希腊裸体像的轮廓,认为这类形体之所以完美,是因为任何一条线都能 在自身中完成,不给观者留下未完之感。 - 曲率连续与自由精神
他把希腊“正面侧影”定为美的典范——颧弓、鼻梁、额头形成连续光滑的线条,既无尖锐折角,也不陷入软弱松弛;正是这种 曲率连续 的“自由流动”显现了人的自由精神。
与“完美曲线”最直接相关的文本坐标
| 卷 / 页码 (Hotho 版) | 主题 | 要点 |
|---|---|---|
| VÄ I §16–21/第一篇“理想” | 理念-感性统一 | 美即理念之感性显现,需在外形上达成“自足闭合” |
| VÄ II “雕塑理想” | 希腊人体轮廓 | “曲线闭合”“肌理张力”=外在曲率表现自由意志 |
| VÄ II “建筑”附注 | 柱鼓(entasis) | 称柱身轻微外鼓为“理性在石材中的生命感” |
| VÄ III “象征·古埃及” | 曲线的不充分 | 纯几何大曲线(圆锥、金字塔)仍显僵硬,未达自由形态 |
阅读提示:Hotho 版序号与其他德文或英文译本可能不同,可用章节名称(Ideal/Sculpture/Architecture)对照查询。
黑格尔如何评价具体“曲线模板”
| 几何母题 | 黑格尔的立场 | 相关出处 |
|---|---|---|
| Golden Ratio 神圣比例 |
未专章讨论黄金分割,但在讲 “内部尺度与外部尺度的自洽” 时提到希腊人用一定比例系统调和整体与细部 | VÄ I §23, §25 |
| Entasis 柱鼓曲线 |
赞赏其“轻度外鼓”消除僵直,体现“生命在石中呼吸”,并把它视作建筑达到“古典自由”的标志 | VÄ II Architecture |
| Ionic volute 卷涡 |
认为柱头螺旋将直立力学与装饰曲线自然过渡,显示理念在对称与动感之间的调和 | VÄ II Architecture, 注释 |
| 希腊人体曲线 | “圆满闭合”与“静中有动”的 S 形是自由精神的可见化 | VÄ II Sculpture |
阅读策略:先读 VÄ I 的“美的理念”,再对照 VÄ II 中“雕塑理想”与“建筑”章的实例;黑格尔“理想曲线”论述多藏在对希腊艺术的长段评述里,可用关键词 Abschluß (闭合)、Krümmung (曲率)、Lebendigkeit (生动) 进行检索|与阿多诺的《美学理论》或温克尔曼《古代艺术史》对照,能看出黑格尔如何把“理想曲线”提升为“绝对精神”的辩证环节。
在黑格尔那里,曲线之“完美”不是数学雅趣,而是 理念 (absolute spirit) 在感性材料中“自由而自足”地闪现。因此每一条经调整的曲线——从柱身外鼓到雕像腰线——都是绝对精神自我肯定的瞬间。
主要参考 & 可用版本
- Stanford Encyclopedia of Philosophy, “Hegel’s Aesthetics”
- Marxists Internet Archive, Lectures on Aesthetics German/English 双语全文
- G.W.F. Hegel, Vorlesungen über die Ästhetik (Hotho ed., 1835) PDF 扫描
- Petry, Hegel’s Philosophy of Greek Sculpture(分析 entasis 与曲率)
- 现代二手解读:Notre Dame Philosophical Reviews, “Houlgate: Hegel on Beauty”

古希腊的完美曲线
在古希腊,建筑师与艺术家用极少量的“弯曲”就让石头与大理石显得完美无瑕——这些隐秘而精准的曲线不仅纠正视觉错觉,也传达了关于秩序、比例与动感的哲学观。最典型的曲线可归为四类:(1)建筑光学修正曲线——柱身 entasis 与基座/檐口的整体弧度;(2)装饰螺旋与叶纹——Ionic volute 和 Corinthian acanthus;(3)圆形/椭圆布局——剧场与圣坛;(4)雕塑与陶器中“黄金”与动势曲线。每一类都成为后世“完美比例”范式的源头。
1 建筑光学修正曲线
| 元素 | 曲线特征 | 目的与实例 |
|---|---|---|
| Entasis(柱鼓) | Doric、Ionic、Corinthian 圆柱在 1∕3–½ 柱高处轻微外鼓,鼓胀率通常 < 1.5 % | 纠正远观“竹竿感”,赋予柱子力量;帕台农 entasis 被誉为最细腻 |
| Stylobate 与檐口上拱 | 帕台农基座沿长边上拱 110 mm、短边 60 mm;檐口同步微弧 | 消除水平“下塌”错觉,使整座神庙在远处看如“漂浮” |
| 整幢无直线 | 探测显示帕台农几乎无真正直线或直角 | 光学完美:每条曲线都在对人眼进行补偿 |
代表性建筑
- 帕台农神庙:柱鼓+基座+檐口三重曲线精调,被视为“石头与几何的协奏”。
- 宙斯神庙(奥林匹亚):尺度更大,仍保持柱鼓—檐弧系统,证明曲线法则已被体系化。
2 装饰螺旋与叶纹
Ionic volute
- 卷涡符合近似对数(多项式)螺旋,可用 r=aθbr=aθ^{b} 拟合;它把圆与直立柱交织成无缝过渡的“视觉缓冲”。
Corinthian acanthus
- Acanthus 叶尖外缘形成重复的圆弧与 S-弯,象征生命与不朽;叶片曲率连续,既利于阴影层次,也便于石雕受力。
3 圆形与椭圆布局
| 类型 | 曲线作用 | 代表 |
|---|---|---|
| 剧场 cavea | Epidaurus 剧场 55 排座椅构成 180° 完整弧;同心圆弧兼顾视线与声学汇聚 | 观众可清晰听见舞台沙声,被誉“声学奇迹” |
| 祭坛/舞蹈场 | 圆形平面象征宇宙秩序,仪式者在圆周旋行 | 德尔菲古祭坛遗迹等 |
4 雕塑与陶器的黄金与动势曲线
| 艺术品 | 曲线精华 | 来源 |
|---|---|---|
| 《掷铁饼者》Myron | 身体像拉开的弓,主视曲线呈抛物弧,体现瞬时动势 | 公元前 460 – 450 |
| Kouros 立像 | 髋部“对角 S 弯”与“阿尔卡イク微笑”让石块显生命感 | 公元前 6 世纪 |
| 典型黑绘 amphora | 肩颈弧与腹弧按黄金比例“分段” | 艺匠以 φ 约 1:0.618:0.382 划分颈、肩、腹 |
| 菲迪亚斯金象 Athena | 披帛褶线用贝塞尔式 S 曲引流光影 | 曲线引导视线聚焦圣像脸部 |
5 几何与审美意义
- 光学补偿:希腊建筑师认识到纯直线在长距离观察会扭曲,因而用毫米级弧度调平水平与垂直感——这是最早的“用户视角设计”。
- 对数螺旋的和谐:Ionic volute 与剧场同心圆体现自然增长律,传递“无始无终”的宇宙观。
- 黄金比例作为符号:在陶器与雕塑中,φ 曲线让人体或器物获得既理性又感性的均衡。
- 曲率连续与结构安全:柱鼓与檐弧的微曲避免应力骤变,也强化纵向载荷抗压——美感与工程并不矛盾。
6 今日启示
- 建筑复原:数字建模需在 NURBS/Bezier 中重现毫米级弧度,否则 “希腊完美”会显得呆板。
- 品牌与 UI 设计:黄金螺旋、超圆角正是古希腊光学补偿在屏幕时代的继承。
- 公共空间声学:Epidaurus 的圆弧座椅启发现代剧场的椭球壳与波束分析。
这些古希腊曲线,既基于精细观测与手工石刻,也暗合后来数学与工程理论——它们跨越 2500 年,依旧是“人眼与理性”共同认可的完美范式。

中国与东方文化
东方文明以“曲”寓“圆”,以“曲”化“直”,将宇宙生成、生命律动与人文秩序浓缩进一条条“完美曲线”之中:从太极 S 曲线到赵州桥扁平拱,从梅瓶的连贯曲率到刀弓的动态反曲,这些形态既满足严格的力学与几何要求,又托举起千年的审美与精神寄托。以下按哲学原型 → 视觉符号 → 建筑空间 → 工艺器物 → 身体之道 → 当代启示六大维度,层层剖面。
一、曲为万象:东方“完美曲线”哲学原型
1. 太极图 S 曲线
- 由两个对数螺旋构成的连续 S 形,将“阴升阳降”的相位变化映射成二维相图,被视为宇宙动静、互根互生的几何隐喻。
2. 圆相(Ensō)
- 一笔成圆,留有“缺口”或闭合,代表“空‧满”辩证与“刹那即永恒” 。
洞见:东西方都尊崇圆,但东方更强调“未完成”“呼吸式”的张力——曲线是动态过程,而非静态轮廓。
二、视觉符号与装饰
1. 如意云纹
- 源自如意柄端的心形/螺旋,演化出“卷草”“云头”连绵纹样,曲率单调递增,符合现代“superspiral”美学。
2. 書法永字八法——“掠、撇、捺”
- 王羲之以单笔曲线揭示“动中寓势”的范式,曲线张力由笔锋速度与腕力控制,与现代样条曲线调参异曲同工。
3. 敦煌飞天与“三道弯”
- 莫高窟第 112 窟的“反弹琵琶”舞姿表现典型 S 曲线,被后世舞蹈家总结为“三道弯”动态范式 。
- 壁画线条“流沙式”连绵,既写实人体也模拟风流云动 。
三、建筑与空间
1. 屋脊飞檐曲线
- 传统硬山、歇山屋顶之檐口呈逐级上翘,研究发现这条“燕尾曲”有疏风、减荷与排水多重功能。
2. 拱桥与月桥
- 赵州桥扁平敞肩拱:全桥主拱跨径37 m、矢高仅7 m,属“超扁圆弧”,并在拱肩开减荷孔,使推力分散,被誉为“力学—美学双完形”。
- 宋元石拱桥的悬链线:拱券曲率接近数学悬链线,受压均匀,被称为“石拱的极限曲线” 。
- “满月”意象:圆拱在水中倒映成整月,含“圆满”祈愿,成为江南园林摄影必拍的“月亮门” 升级版。
3. 园林曲线
- 太湖石:天然侵蚀留下“皱、漏、瘦、透”四字诀,每一条虬曲都是“山川缩影” 。
- 洞门与葫芦门:门洞边线常把直、曲“折中拼接”,如意、瓶门、海棠门用连续曲段制造“曲径通幽” 。
四、工艺与器物
1. 梅瓶(Meiping)
- 从底到肩曲率连续变化,曲率极小值位于瓶颈过渡区,呈“C³ 光顺”级别,被称为“陶瓷中的贝塞尔曲线” 。
2. 古琴“蕉叶式”面板弧
- 面板纵剖呈抛物线—圆弧复合曲线,赋予泛音共振与手感平衡。
3. 刀与弓——动势曲
- 日刀‧Sori:根据受力点不同分“Koshi-zori/腰反”“Saki-zori/先反”等,多样曲率优化了拔刀顺滑与劈砍角度。
- 汉弓‧Recurve:静态反曲耳头释放储能,提升射速且缩短弓身,古称“神臂” 。
五、身体与道法
- 太极拳圆弧步、弓步弧腰皆要求丹田为圆心划“立体八卦”,强调“劲走弧道”;剑舞“燕回旋”则以刀身曲率映射人体运动学,对应现代生物力学中的“最小肌群功曲线”。
- 旗袍 S 曲线:20 世纪 30 年代改良旗袍收腰、高衩,令布面与人体一起形成“S 曲线—直线—S 曲线”节奏 。
六、当代启示:未来设计的“东方曲率”
- 减荷技术:赵州桥的开孔思想被移植到超长跨拱桥与轻量化航空桁架。
- 参数化遗产:屋檐“燕尾曲”正通过算法优化转化为高铁车头、体育馆双曲面壳体。
- 情感曲线:梅瓶与如意云纹的连续曲率美学,正在 XR 界面与 AI 生成曲面建模中提供“情感光顺”模板。
参考资料
- 太极几何与相位图 (科学直达, Medium)
- 屋顶曲线风压研究 (科学直达)
- 赵州桥力学分析 (ResearchGate)
- 梅瓶形制 (Weisbrod Collection)
- 月洞门象征 (Improve Your Chinese)
- 如意纹源流 (Wikipedia, Atlantis Press)
- 刀身曲率 Sori (Tozando Katana Shop)
- Yumi 弓非对称曲 (Wikipedia)
- Zen Enso (ChangYoga – Home)
- 古琴面板曲率 (Organology)
- 中国弓反曲技术 (thewayofarchery.com)
- Dou-gong 分荷曲线 (forestsong.inkedblade.net, polyglottando.com)
- Lotus Mandala 曲式 (Rubin Museum of Himalayan Art)
- Sacred Lotus-curve象征 (Janis Lava Mandalas)
建筑
在建筑史上,“完美曲线”常被用来解决受力、声学或动线难题,也常被视为精神象征与审美追求。纵观古典到当代,可归纳四个关键阶段:古典穹顶与细部弧线 → 中世纪/文艺复兴的空间几何实验 → 现代主义的流线结构 → 当代数字化自由曲面。下面精选 12 座里程碑建筑,说明它们如何以曲线创造技术与美学的双重极致。
古典时代:曲线确立空间神圣感
| 建筑 | 曲线要点 | 年代 |
|---|---|---|
| 帕台农神庙 | 柱身“轻度鼓胀”(entasis)与檐口上翘的弧线微调,校正视觉畸变,被誉为“几何幻觉”杰作 | 公元前 447–432 |
| 罗马万神殿 | 43.3 m 完整半球穹顶与 oculus 构成“地表最大完美圆”,示范无筋混凝土薄壳的极限 | 118–128 AD |
| 圣索菲亚大教堂 | 四只“悬链线”形抛物拱+ Pendentive过渡,使31m穹顶似浮空,首创大跨“曲面壳”体系 | 532–537 |
中世纪至文艺复兴:几何学与宗教空间的结合
| 建筑 | 曲线要点 | 年代 |
|---|---|---|
| 哥特花窗(沙特尔大教堂西玫瑰窗) | Reuleaux 三角与多弧 tracery 组合展示常宽曲线在宗教象征与结构减重中的应用 | 13 c. |
| 圣彼得大教堂圆顶(米开朗基罗方案) | 双层薄壳,曲率渐变控制推力,外观与结构完美统一 | 16 c. |
现代主义:流线形与工程逻辑
| 建筑 | 曲线要点 | 年代 |
|---|---|---|
| 古根海姆纽约馆(弗兰克·劳埃德·赖特) | 单螺旋坡道+抛物圆筒外壳连贯观展流线与结构受力 | 1959 |
| 悉尼歌剧院(约恩·乌松) | 所有壳体来自同一球体切片,解决复杂曲率制造难题,被称“球面解” | 1973 |
| MIT Kresge Auditorium(埃罗·沙里宁) | 1/8 球壳+三点支撑的超薄双曲壳,演示 HP 曲面极限 | 1955 |
| TWA Flight Center(沙里宁) | 混凝土薄壳四翼似振翅之鸟,流线曲线统合结构与品牌意象 | 1962 |
当代数字化自由曲面
| 建筑 | 曲线要点 | 年代 |
|---|---|---|
| 慕尼黑奥林匹克体育场(弗莱·奥托) | 张拉膜屋面形成连续鞍形曲面,首次把“最小曲面”引入超大跨屋盖 | 1972 |
| 梅赛德斯-奔驰博物馆(UNStudio) | 双螺旋 DNA 曲面纵贯九层,流线导览与结构梁网同步生成 | 2006 |
| 海达尔·阿利耶夫中心(扎哈·哈迪德) | 自由曲面连续折返,参数化控制曲率与面板尺寸,被誉“流体白丘” | 2012 |
| 高迪圣家堂(持续建造中) | 反吊链模型确定 catenary & 双曲抛物面塔体,实现自然力学曲线的宗教图腾 | 1883– |
为什么它们被视为“完美曲线”的里程碑?
- 结构极限验证:从万神殿无筋混凝土半球到奥托最小曲面膜,曲线被用来最小化推力、材料与自重。
- 几何-感知协同:帕台农 entasis、沙里宁薄壳与扎哈自由曲面皆通过精细曲率分布,消除视觉畸变并引导人流。
- 技术创新驱动美学:每一次材料或算法革新(罗马混凝土、20 世纪薄壳、21 世纪参数化)都会催生新的“完美曲线”范式。
- 符号与情感:无论宗教穹顶还是 DNA 螺旋,曲线形态被赋予宇宙、生命或速度的隐喻,为观者提供超越功能的精神框架。
这些建筑不是简单追求“炫技”曲面,而是在结构理性、制造技术与文化象征三条轴线上找到最优交点,因而成为“完美曲线”在建筑史的经典注脚。
绘画
在艺术史的长河里,许多画家用“几乎数学般精准的曲线”来象征和谐、动感或精神境界——从文艺复兴对几何比例的迷恋,到现代主义对纯粹形式的礼赞。下文按时代与流派精选十幅作品,展示“完美曲线”如何跨越文化与媒材成为视觉焦点,并简述其观念价值与背后几何逻辑。
1 文艺复兴:几何理性的复兴
1.1 波提切利《维纳斯的诞生》(1484 – 86)
维纳斯与海蚌共同构成一条优雅的 S 形曲线;风神与接引女神的披风弧度把目光导回主角,产生近似“对数螺旋”的动势。
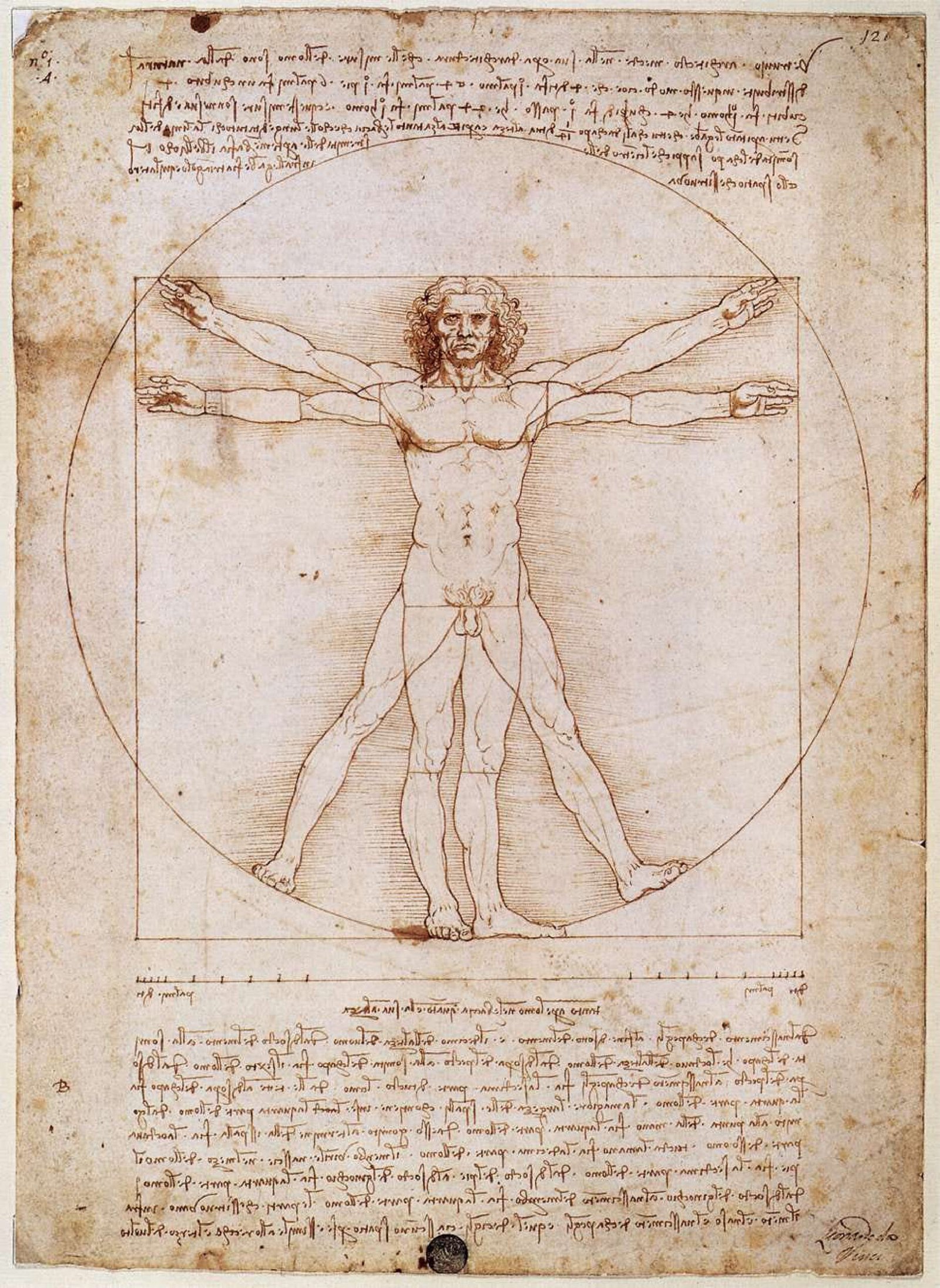
1.2 达·芬奇《维特鲁威人》(约1490,素描)
人体双重站姿同时嵌入正方形与圆,暗示“恒定曲率的圆”是人—宇宙比例的终极公设。
1.3 拉斐尔《椅中圣母》(1514)
整幅画采用 tondo(圆形画面);圣母-圣婴-施洗者三人旋成漩涡式曲线,借圆形边框放大“完美母性”的和谐感。
2 浮世绘:黄金螺旋的惊涛
葛饰北斋《神奈川冲浪里》(1831)
主浪弯爪呈现接近黄金螺旋的反卷弧度,与远处圆锥形富士山形成大小呼应,被认为是自然界“自相似曲线”在二维平面的典范。
3 新艺术运动与象征主义:装饰化的流线
3.1 阿尔丰斯·慕夏《黄道十二宫》(1896,海报)
人物发丝与花环以长鞭式曲线环抱主像,体现 Art Nouveau “鞭形线条”强调的植物生长律动。
3.2 古斯塔夫·克里姆特《吻》(1907–08)
金叶装饰与人物颈部拱弧构成连续欧拉曲线;曲线包围方形图案,形成圆-方二元并置的象征张力。
4 现代主义:形式纯化与身体释放
4.1 亨利·马蒂斯《舞蹈》(1910)
五位舞者手-足-躯干连成近乎完美的圆周,整个构图只有两条主曲线即可闭合;马蒂斯借此宣告“色块+完美曲线”即可创造原始生命力。
4.2 瓦西里·康定斯基《构成 VIII》(1923)
画面密布圆、弧与抛物线等几何曲线;康定斯基视其为“精神性音符”,证明抽象也能依赖“曲率逻辑”组织节奏。
5 20 世纪后半:感官与光学的极致
5.1 乔治亚·欧姬芙《曼陀罗花 No.1》(1932)
巨幅花瓣以同心弧推进,柔滑曲线把微观花蕊放大到近乎宇宙漩涡的尺度,重新定义“女性曲线”意象。
5.2 布里奇特·赖利《火焰 4》(1964)
黑白放射弧阵列诱发强烈位移错觉,说明“完美而重复的弧线”可直接作用观者视皮层,成为欧普艺术经典。
6 意义与启示
- 几何即叙事:从拉斐尔的圆形圣母到赖利的光学晕眩,完美曲线不断被用来讲述和谐、动势或神秘秩序。
- 跨文化共鸣:无论佛罗伦萨、江户还是巴黎,艺术家都不约而同地把黄金螺旋、恒曲率圆或流线鞭形视为“优雅捷径”。
- 感官+理性双重快感:心理学研究表明,恒定或单调曲率曲线最易触发“认知流畅”;因此观众在这些作品中直觉感到“自然且完美”。
- 当代创作参考:理解这些经典如何部署“完美曲线”,可为 UI 设计、品牌符号、建筑曲面提供可复用的几何母题。
透过上述十例,我们看到“完美曲线”并非单一风格标志,而是一条贯穿人类视觉文化的隐形逻辑:它既满足比例与曲率的理性要求,也让观者的目光和情绪在流动中获得最大自由。
音乐与声音
在音乐与声音世界,几乎一切可听的“美” 都能还原成曲线——声波本身的振幅-时间轨迹、包络线的缓升急降、旋律的起伏走向、听觉系统的等响度轮廓,乃至压缩器“软-硬膝”或 DAW 自动化里的 Bézier 轨迹。本质上,声音之美=曲线形态与人耳/情感/物理之间的契合。下文依“波形-包络-音高-响度-动态-可视化-自动化”七条主线,系统梳理音乐中最具代表性的“完美曲线”及其设计、感知与工程价值。
1 波形原型:音色美学的几何根
Sine—Square—Triangle—Saw
- 正弦波无谐波,曲线最光滑,被称为“声音的素描纸”(perfectcircuit.com)。
- 锯齿波呈线性斜坡+突降,曲率不连续却为富谐波音色奠基。
启示:音色设计常以正弦作“母线”,再通过 FM/滤波在曲线上增加“纹理”。
2 包络线:动态流畅的 ADSR 曲线
- ADSR(Attack-Decay-Sustain-Release)用四段线性/指数段定义响度曲线,是合成器“生命呼吸”(WolfSound)。
- 高级包络可用二次 Bézier或六段 AHDSR,曲率连续减少电平突兀(Unison)。
3 旋律与音高轮廓
- 心理学将“melodic contour”视为旋律可记忆性的关键:升-降曲线越流畅,越易被辨认(PMC)。
- 演唱中的vibrato是 5–7 Hz 的正弦调频曲线,既增强情感,又避开频率遮蔽(music.arts.uci.edu)。
4 响度感知曲线:Fletcher-Munson 等响度
- 等响度曲线显示:人耳对 3 kHz 左右最敏感,低频需更高 SPL 才等响(维基百科)。
- 现代母带会参考 ISO 226:2003 曲线微调 EQ,以“曲线补偿”获得主观均衡。
5 动态处理:软膝-硬膝压缩曲线
- Knee 曲线决定阈值附近压缩比的平滑度:软膝曲线弯圆过渡,更“自然”(Pro Audio Files, Signal Processing Stack Exchange);硬膝拐点尖锐,适合打击感(uaudio.com)。
- DSP 实现常用二次插值保 C1C^1 连续,避免谐波失真(Signal Processing Stack Exchange)。
6 可视化曲线:让声音“看得见”
6.1 Lissajous 图形
- 直角 XY 示波绘制左/右声道,可立即发现相位偏差,其几何优雅长期吸引 VJ (音频大师班)。
6.2 Spectrogram
- 频率-时间-强度三维曲面揭示声谱“山脊”与谐波曲线,被称为“声学地形图”(维基百科)。
7 自动化与合成中的 Bézier / Catmull-Rom 曲线
- 现代 DAW 允许用 Bézier 把手绘制音量、滤波、声像自动化,曲率平滑免除“点-线阶梯”爆音(KVR Audio)。
- 实时路径插值常用 Catmull-Rom 保证穿点且无过冲,用于粒子合成与波表混音(音频大师班)。
8 作曲与演奏中的动态曲线
- 记谱 < >(hairpin)提示crescendo/decrescendo;指挥家常将其演绎为指数曲线而非线性斜率,以契合人耳响度感知(Reddit)。
9 设计“完美声音曲线”的实用准则
- 曲率连贯:避免 1 dB 以上突跳——包络或自动化中采用指数或 Bézier。
- 对耳匹配:参考等响度曲线,低频渐变需更长包络。
- 物理-情感协同:vibrato 深度≈±50 cent,速率≈6 Hz 最易触发情感共鸣(music.arts.uci.edu)。
- 可视反馈:在 Lissajous 或频谱曲面上实时监看,任何“曲线折角”往往对应听感尖刺。
通过正弦与 ADSR、vibrato、等响度、软膝压缩、Bézier 自动化等多维曲线的协奏,声音得以在物理规律、人耳生理与情感审美之间达成平滑、自由且精准的平衡。掌握并精修这些曲线,正是音乐制作与音频工程走向“听觉完美”的关键。
味道
现代感官科学把“味道”拆解成 浓度-时间-愉悦 的多维曲线:每一道菜、每一杯饮品,乃至食品加工环节里一分一秒的温度与成分比例,都会在口腔与大脑里描出可量化的波形。所谓“完美味道曲线”,就是把这些波形调校到——释放节奏顺滑、峰值精准、余韵干净且整体让人愉悦。下文分四条主线(时间-强度、热加工、风味平衡、感官模型)梳理最具代表性的曲线范式,并给出设计与测量要领。
时间-强度:味道“登顶→回落”的黄金轨迹
感官学的 “Time-Intensity” 曲线
- 现代品评采用 TI 曲线 追踪单一味质的即刻感知、峰值与衰减;优质橄榄油等乳化体系可呈现“快速上升-宽平台-缓跌”理想形态,带来持续而不滞腻的口感 (科学直通车)。
- 人体对甜味、酸味等呈现明显延迟-衰减模式,完整曲线常用 LOESS 或样条平滑后进行对比分析 (Frontiers)。
味觉强度-浓度响应
- 谷氨酸钠(MSG) 的“鲜味曲线”在 0–1.2 g/100 mL 区呈对数抛物趋势,超过阈值反而降低整体愉悦度——典型 倒 U 型 曲线 (ResearchGate)。
- 甜味的 享乐曲线 亦呈倒 U 型,高浓导致“甜腻厌恶” (PMC)。
热加工曲线:火候与反应速率的完美叠合
Maillard 反应的“钟形曲线”
- 味精、还原糖与蛋白在 120–180 °C 区间进入高活跃期;温度-时间可视为“滑竿”,两端都产生欠熟或焦苦味,最佳窗口在中心 (FireBoard Labs, Serious Eats)。
- 同理可揭示烘焙、煎烤肉类中褐变-香味与苦味生成的平衡 (PMC)。
咖啡烘焙“发展/烘黑”曲线
- 咖啡师用 RoR(Rate-of-Rise) 曲线确保“干燥-梅纳-发展”三段稳步升温:RoR 过冲会造成草味,过低则平淡 (mtpak.coffee);专业软件以曲线回放对比批次一致性 (完美每日研磨)。
啤酒苦味 IBU-利用率曲线
- 三种模型(Tinseth、Rager、Garetz)皆以 煮沸时间 为 X 轴呈 渐饱和曲线:30–45 min 后苦味提取趋平,继续延长仅增加草本涩味 (beersmith.com)。
风味平衡曲线:酸-甜-苦-鲜的协奏
| 应用 | 关键曲线 | 设计原则 |
|---|---|---|
| 红、白葡萄酒 | 糖-酸 “对角平衡”曲线:同糖度下酸度越高 perceived 甜度越低 (The Mill Keeper, Food & Wine) | 酸:糖 ≈1:2 常被视为清爽阈值 |
| 高汤、酱汁 | 鲜味(谷氨酸)与盐度呈 交互放大曲线:低盐时鲜味增感,超阈后鲜味被掩蔽 | 0.3–0.5 % NaCl + 0.05 % MSG 为多数汤品黄金比 |
| 巧克力 | 可可固形+Brix 与苦味曲线交叉点决定“甜-苦平衡” | 60–70 % 黑巧在倒 U 曲线上既有果酸又保留可可香 |
曲线的测量与建模工具
感官-数据双轨
- 电子舌/鼻 + TI 软件:秒级记录电导/挥发物强度,输出平滑曲线。
- Panel TI 打分:人工在 0–100 s 连续打标,后用样条/贝塞尔重建曲线。
可视-可控-可复制
- R/Python 用
ggplot2::stat_smooth或scipy.signal.savgol_filter作曲线拟合,检视峰值位置与半峰宽。 - 工业 4.0 线控锅或智能烘焙炉内嵌 PID 曲线与算法回放,实现配方-曲线数据库化。
小结
味道的完美曲线 = 在时间轴上精准排布“生成-峰值-衰减”,并让强度-浓度落在“倒 U 型”愉悦区;在热加工时把温度-时间滑到 Maillard 的最佳窗口;在配方层面用酸-甜-苦-鲜的交互曲线锁定平衡点。 通过传感器与算法把这些曲线量化、回放与微调,厨师、烘焙师或饮料开发者就能把风味稳定地推向“黄金轨道”。
查阅来源
- Development and use of time-intensity methodology for flavored emulsions (科学直通车)
- Frontiers: sweet TI profiles & pleasantness (Frontiers)
- MSG umami强度响应曲线研究 (ResearchGate)
- Sweet taste hedonic curve个体差异综述 (PMC)
- Maillard Reaction: time-temperature sweet spot (FireBoard Labs)
- Serious Eats:Maillard browning条件 (Serious Eats)
- Review on flavour-driving factors of Maillard reaction (PMC)
- Roast curve与咖啡风味预测 (mtpak.coffee)
- Perfect Daily Grind:烘焙曲线三阶段 (完美每日研磨)
- BeerSmith:Hop utilization模型曲线 (beersmith.com)
- Wine酸-糖平衡 (The Millkeeper) (The Mill Keeper)
- Food&Wine: acidity组织风味曲线 (Food & Wine)
- ISO 等响度及味觉敏感度背景 (FireBoard Labs)
可以触摸的完美曲线
在可被双手抚摸、把玩或倚靠的世界里,“完美曲线”是 曲率连续、无尖点、在视觉与触觉上同时舒适 的形态——它们把数学优雅转译成真实的手感:贴合手指的 iPhone 超圆角、环绕手腕的 Bulgari Serpenti 螺旋、顺着脊柱弧度的 Eames Lounge Chair、指尖能感到流动张力的 Georg Jensen Möbius 戒指,乃至大理石般光滑的 Rodin 与 Brancusi 雕塑。以下按 日常产品 → 珠宝首饰 → 家具设计 → 汽车/家电外壳 → 雕塑建筑 五大触觉场景梳理代表性“可触曲线”,并解读它们如何通过曲率优化、材料工艺与品牌叙事,实现“看得美、摸得爽、用得久”的多重完美。
日常产品:随身携带的超圆角与对数弧
| 物件 | 曲线范式 | 触感密码 | 典型来源 |
|---|---|---|---|
| iPhone / iPad 外壳 | 可变半径超圆角(super-ellipse blend)使曲率在边—面间平滑过渡 | 握持时无“割手点”,指腹滑动不觉突兀 | 苹果圆角几何揭秘讨论指其半径越接近直边越大 |
| Dyson Air Multiplier 环形出风口 | 连续圆环 + 7° 航空翼形斜坡 | 碰触仅感微温光滑,无叶片割手;封闭环也更安全 | Dyson 官方风扇仿真资料 |
珠宝首饰:螺旋、环带与恒曲率
| 物件 | 曲线 | 触觉与象征 | 典型来源 |
|---|---|---|---|
| Georg Jensen Möbius Ring | Möbius 单面环带,κ 连续 | 环内外无可察边缘,象征永恒与一体 | |
| Bulgari Serpenti 手镯 | 对数螺旋节片 | 金属节距渐缩,贴肤同时能自由弯曲 |
家具设计:贴合人体的 S-弯与多半径壳体
| 物件 | 成名曲线 | 触感亮点 | 典型来源 |
|---|---|---|---|
| Eames Lounge Chair | 三段可变曲率胶合板壳 | 靠背弧度与脊柱自然贴合,边缘倒角无骨点(Time) | |
| Georg Jensen Wave 托盘 | 单调 S-弯 | 扶手处无角,握持时手掌压力均匀 |
汽车与家电外壳:流线飞弧与“握持半径”
| 领域 | 曲线符号 | 触觉/品牌作用 | 典型来源 |
|---|---|---|---|
| Porsche 911 侧窗飞线 (flyline) | 从 A-柱滑到尾部的抛物长弧 | 手滑过车顶边缘感受连续流线;曲线几乎未改动 60 年 | |
| Reuleaux Spinner 把玩器 | 恒宽三角圆弧 | 拇指在曲面上可 360° 平滑滚动,无停顿 |
雕塑与建筑:石头里的“触觉流线”
| 作品 | 曲线说服力 | 触觉体验 | 典型来源 |
|---|---|---|---|
| Rodin《吻》、《思考者》 | 肢体肌肉曲率渐变 | 石膏/青铜抛光后抚摸如活肌(The New Yorker) | |
| Brancusi《Bird in Space》 | 由底到顶连贯加速的纺锤曲线 | 把手从底座滑到尖端,感到线条“加速” | |
| Gaudí Casa Milà 石波立面 | 自由波浪曲线 | 游客手扶花岗岩栏杆感到无重复的起伏 |
为何这些曲线“摸”得完美?
1 曲率连续 = 无割裂触感
边-面过渡用可变半径或 Bézier 混合,让 κ′≈0;手指/手掌不会遇到突跳。2 恒宽或单调曲率 = 压力均匀
Reuleaux 恒宽与 Möbius 环带让压力沿曲面分散,避免“压痛点”。3 材料工艺放大曲线优势
金属抛光、胶合板层压、玻璃注塑等技术,把数学曲线译成无缝、可长时间触摸的表面(Time)。4 品牌叙事:一条线即身份
Porsche flyline、Bulgari 螺旋等曲线成为品牌独特触感签名,几十年不变。
触觉完美曲线的设计要点
- 先看曲率梳:CAD/NURBS 中保持 κ 连贯;尖峰>2σ 需调控制点。
- 按人体接触半径倒角:手机边≥2 mm;家具木边≥5 mm;金饰内圈≥0.5 mm。
- 材料—曲线匹配:高硬度材料用更大曲率,防止“割手”;软材可用小半径。
- 快速原型验证:3D 打印或 CNC 蜡模后做盲触测试,记录压力分布,再微调控制点。
小结:从手中的手机、腕间的珠宝,到可以拥坐的椅子、抚摸的大理石雕塑——“触摸得到的完美曲线”总是 曲率连续、压力平滑、表面细腻且伴随深层品牌/情感寓意。它们把抽象几何(超圆角、螺旋、恒宽、Möbius)与人体工学、材料技艺完美融合,成就既可审视也可抚爱的极致形态。
工业设计
在工业设计史上,“完美曲线”往往同时满足 功能学上的极简高效 与 审美上的流畅和谐。下表式盘点 10 件跨世纪的代表性产品——从饮料瓶到刀具——它们用精准的几何曲线解决结构、握持、空气动力或品牌识别问题,并因此成为各自行业的“黄金范本”。
包装 / 饮料
| 经典曲线 | 设计要点 |
|---|---|
| 可口可乐“Contour Bottle” | 双曲率“S”形连贯过渡,瓶颈—瓶腰—瓶底无断点,被雷蒙德·洛威称为“最完美的液体包装” |
消费电子
| 经典曲线 | 设计要点 |
|---|---|
| iPhone/Apple Watch 圆角 | 采用可变半径超圆角(super ellipse blend),曲率随距离边缘逐渐增大,消除直线-圆弧折感 |
| Apple Magic Mouse | 整体仅由一块多向双曲面玻璃+一块铝底组合,侧向曲线确保握持与多指滑动手势顺滑 |
汽车交通
| 经典曲线 | 设计要点 |
|---|---|
| Volkswagen Beetle | 整车轮廓由一条连贯圆拱包围,提供最大车内空间与亲和“面部”表情 |
| Porsche 911 “Flyline” | 从 A 柱顶点一路滑向尾部的单条抛物曲线,被保时捷官方反复强调为 DNA 核心 |
家电 / 餐厨
| 经典曲线 | 设计要点 |
|---|---|
| Dyson Air Multiplier | 窄缝圆环产生均匀诱导气流;闭合环形曲线既降低湍流噪音又成品牌符号 |
| Alessi 9093 鸟鸣水壶 | 壶身采用截顶球面,壶嘴—把手曲线呼应 Art Deco “流线 (streamline)”美学 |
家具与人体工学
| 经典曲线 | 设计要点 |
|---|---|
| Eames Lounge Chair (LCW) | 热压弯曲胶合板形成连续坐、背弧;曲率源于脊柱生理曲线,1960 年被《Time》评为“20 世纪最佳设计” |
| Opinel 刀柄 | 山毛榉木柄按手掌鱼腹曲线 (belly curve) 镂铣,握持点曲率单调递减防疲劳 |
| Gillette Razor & 女士 Venus | 剃头外壳为多半径圆角,柄部波浪曲线递进匹配掌心、人鱼线,结合可旋转“圆弧刀头” |
为什么这些曲线被视作“完美”?
- 单调或恒定曲率 → 视觉与触觉流畅:苹果超圆角、Eames 胶合弧及 Alessi 壶身都避免曲率跳变,带来无意识的“认知流畅”体验。
- 结构-功能最优:VW Beetle 圆拱抗压强、Dyson 闭环降低湍流,说明“好看”并非牺牲性能。
- 品牌图腾化:可口可乐瓶曲线比商标更易被全球识别;Porsche flyline 数十年不改即是典范。
- 制造与材料革新驱动:弯曲胶合板、数控铝合金、热塑玻璃、流体仿真等技术把复杂曲线从“概念草图”变成批量产品。
在工业设计里,一条“完美曲线”往往是“性能边界 + 制造极限 + 情感符号”多重博弈的产物,它让物品在手感、视觉与功能三条维度同时达到高峰,因而历久弥新。
图形设计
在图形设计领域,“完美曲线”≈曲率连续又语义精确的形态,它们让 Logo 、字体、UI 圆角与动效既顺滑又易于品牌辨识。无论是贝塞尔与 NURBS 的精确控制、黄金螺旋带来的视觉均衡,还是苹果可变半径圆角与 D3 单调插值的防过冲策略,背后都隐藏着可量化的曲率原则与工具链。下文先阐释六条核心曲线范式,再给出从草图到 AI 抛光的工作流与典型案例,帮助你把“完美曲线”落实到日常设计。
1 六条常用“完美曲线”范式
1.1 Bézier / B-Spline(基础)
- 二次、三次贝塞尔通过 De Casteljau 算法实现 Cn−1C^{n-1} 连续,是 Adobe Illustrator 与 SVG 路径的基石(Linearity)。
- NURBS 把权重引入 B-Spline,可建模圆、螺旋等解析曲线,用于工业级 Logo & 产品曲面。
1.2 黄金螺旋 / 𝜙 比例
- 137.5° 等角生长避免视觉拥挤,常用于标志排布(Twitter 鸟、Pepsi 2009 新版)(Adobe Stock)。
- 对数螺旋在品牌图形中营造“生长”和“动感”隐喻。
1.3 可变半径超圆角(Super-ellipse Blend)
- iOS 图标、Apple Watch 表壳使用半径递增的超圆角,使直边→圆角转变无切线突跳(Reddit)。
1.4 Catmull-Rom / Monotone Cubic
- 交互折线或渐变 Blob 常用 Catmull-Rom 生成穿点曲线;若需防“超调”,改用 D3 的 Monotone Cubic Hermite(Reddit, observablehq.com)。
1.5 光学补偿曲线(Typography Overshoot)
- 圆形字母需超出基线 1–2 %;三角字母需更高“尖角外伸”以获得等视粗细(Medium)。
1.6 Easing 曲线(Motion Design)
- bezier-easing 曲线控制“slow-in & slow-out”,让动效具备物理可信度;常见预设:ease-in-out-cubic、expo、back 等(Hanson Inc. Blog)。
2 设计流程:从草图到曲率梳
2.1 草图 → 矢量化
- 手绘草图扫描。
- Illustrator Curvature Tool 快速布点,初步成 Bézier 路径(YouTube)。
2.2 曲率诊断
- 在 AI、Rhino 或 Figma Plug-in 打开 curvature comb;剔除 κ 突刺点。
- 指标:κ′(曲率变化率)< 0.05 px⁻² 一般被视为“肉眼无伤感”。
2.3 微调与导出
- 角落过硬 → 改超圆角参数;折线过多 → Catmull-Rom 重采样。
- 导出 SVG / PDF,保留控制点,方便前端或印刷继续无损缩放。
3 AI & 可微抛光
| 方案 | 思路 | 参考 |
|---|---|---|
| BézierGAN | GAN 直接生成控制点序列,实现 Logo/图标的“一键顺滑”(arXiv) | PyTorch + SVG 输出 |
| DeepSpline | Transformer 输出节点向量,自动拟合草图轮廓 | 设计草图矢量化 |
| 可微 SDF | 把曲率正则写进损失 λ∫(k−k0)2ds\lambda\int(k-k_0)^2 ds,自动抹平锯齿 | Neus / Diff-SDF (Medium) |
4 典型应用案例
| 场景 | 曲线策略 | 成果 |
|---|---|---|
| 品牌 Logo | 黄金螺旋 + Bézier 超圆角 | Twitter、National Geographic |
| UI 圆角 | Apple Super-ellipse | macOS 窗口、iOS 图标 |
| 信息图线图 | Monotone Hermite | D3.js “smooth line” 模式 |
| 动效 Path Morphing | Catmull-Rom + ease-in-out 曲线 | SVG blob loading 动效 |
| 字体 Optical 调整 | Overshoot 曲线 & humanist 弧 | Helvetica、Futura 圆体 |
5 实战技巧与误区
- 误用恒圆角:屏幕小图标易显“方”,用可变半径超圆角替代固定 20 px 半径。
- 过拟合曲线:控制点过多导致文件臃肿;用 Simplify Path & Catmull-Rom 精简,再检查 κ 变化。
- 忽略动态图形曲率:SVG path 动效若关键帧差大曲线爆破;先 tween 控制点,再 tween 样条。
小结
完美曲线在图形设计 = 贝塞尔精度 × 黄金比例平衡 × 曲率梳校正 × 可微 AI 抛光。用数学与工具把视觉直觉“翻译”成 κ(s) 连续的路径,你就能让 Logo、字体、UI 角与动效在任何分辨率下都保持丝滑、克制而令人难忘。
家具与家居陈设
在家具与家居陈设领域,“完美曲线”往往意味着:曲率连续、手感顺滑、结构高效、情感符号强烈。从 19 世纪蒸汽弯木到 21 世纪参数化建模,设计师借助不同材料与工艺,让曲线兼顾人体工学、制造极限与视觉诗性。以下从 “设计原则 → 经典范例 → 技术幕后” 三个方面,梳理如何在家居环境中呈现这些极致曲线。
设计原则:把曲线变成体验
- 单调或恒定曲率——触感与视觉的流畅
- Apple 等品牌在边缘采用 可变半径超圆角,曲率渐变避免折线感,手指划过毫无停顿。(Arne Jacobsen)
- 经典木作椅背常用 Bézier 曲线 或 G² 连续样条,让脊柱与家具接触压力均匀,久坐不累。
- “一笔成形”——让结构与造型合一
- 曲线即品牌符号
-
- 可口可乐瓶在包装业如此,家具里则有 Porsche 911 的 fly-line 与 Vladimir Kagan Serpentine 沙发:一条识别度极高的轮廓线可持续半个世纪。(弗拉基米尔·卡根官网, vitra.com)
经典范例:10 件曲线传奇
| 类别 | 作品 & 设计年份 | 曲线亮点 | 室内呈现要领 |
|---|---|---|---|
| 弯曲胶合板 | Eames Lounge Chair & Ottoman (1956) | 三段可变曲率胶合壳体包裹人体 | 与柔软织物或皮革搭配减轻木质硬感 (赫尔曼·米勒) |
| 整体发泡壳体 | Egg Chair – Arne Jacobsen (1958) | 双曲率蛋壳围合私密声场 | 常置于开敞空间形成“声学避难所” (Arne Jacobsen) |
| 一体成型塑料 | Panton Chair (1960) | 连续 S 形 + 悬臂受力 | 成排陈列时曲线产生“流动墙”效果 (vitra.com) |
| 雕塑基座 | Noguchi Coffee Table (1944) | 3 片互锁木弧撑起自由玻璃面 | 玻璃映射弧形阴影,放大雕塑感 (store.hermanmiller.com) |
| 蒸汽弯木 | Thonet No. 14 (1859) | 圆环扶手以单根榉木热弯 | 轻质且易堆叠,为餐饮空间增动态节奏 (thonet.de) |
| 自由曲面沙发 | Serpentine Sofa – V. Kagan (1950) | 无前后之分的波浪曲线 | 作为“岛屿”布置,引导环形动线 (弗拉基米尔·卡根官网) |
| 参数化层叠 | CNC 层片书架/屏风 | 每片轮廓略变,整体呈最小曲面 | 兼作隔断与装饰,“可视声学”双效 (Pinterest) |
| 自然主义木椅 | 高迪 Casa Batlló 椅 (1906) | 椅背与人脊柱凹凸完全贴合 | 结合暖色灯光凸显木纹流线 (casabatllo.es) |
| 流体复合材料 | 扎哈·哈迪德 “Moonsoon” 座椅 (1992) | 玻璃钢一次拉模,曲线似水波 | 适合极简空间作雕塑焦点 (Architectural Digest) |
| 环形空气动力 | Dyson Air Multiplier (2009) | 闭合环形喷嘴+文丘里效应 | 曲线本身即为功能话语 |
制造技术:曲线落地的工艺密码
- 蒸汽热弯
榉木加压蒸汽后在金属胎具中定型,形成半径<30 mm 的圆弧且纤维不断裂,是 Thonet 等弯木家具的核心技术。(thonet.de) - 层压胶合 / 热压模
多层单板+脲醛胶在雕刻模具中受热压,获得可变曲率壳体(Eames、Noguchi 均用此法)。纤维方向交错,强度优于实木。(赫尔曼·米勒) - 玻璃钢 / 注塑一体
Panton 椅最早用玻璃纤维增强聚酯,后期改为聚丙烯注塑,一次成型即可获得连续曲面与中空加强肋。(vitra.com) - 数控分层 / 曲面拼壳
当代参数化家具常将 NURBS 曲面离散成若干剖面片或异形瓦片,数控切割后滑槽拼装,既经济又易运输。(Pinterest)
为什么这些曲线被视作“完美”?
- 节奏与对比:用一件曲线家具打破硬朗直线的墙体和地面,可在空间中制造“流动焦点”。
- 成组布局:同系列曲线椅成排,或曲线沙发与圆形地毯配合,增强视线引导。
- 光影强化:侧向洗墙灯能在弧面上形成渐变高光,凸显曲率;玻璃或抛光塑料桌面映射曲线阴影,增添层次。
- 人体工学优先:曲线不是装饰,而是让腰背、手肘、掌心真正“找到落点”。选购时测试多姿态坐感是关键。
家具与家居陈设中的“完美曲线”绝不仅仅是视觉符号;它是材料、工艺、人体、品牌与空间动线的多维协同。理解经典之所以流传的曲率逻辑与制造密码,才能在当下的数字化工具里继续演绎出属于自己的“完美曲线”。
首饰设计
人类用首饰这门“小尺度雕塑”反覆诠释 “完美曲线”——从 19 世纪弯木首饰到 21 世纪参数化黄金,一条精准而流畅的轮廓同时决定 佩戴舒适度、结构强度、光线反射、情感符号。下文按“历史范式 → 当代标志 → CAD/AI 工艺 → 人体学与品牌策略”四段,对最具代表性的首饰曲线作系统索引,并给出生成与评估要点。
历史范式:四条经典母题
| 时代/流派 | 典型作品 | 曲线特征 | 链接美学/技术 |
|---|---|---|---|
| Art Nouveau (1890-1910) | Lalique、Van de Velde胸针 | “Whiplash” S 弧大幅摆荡,曲率单调递增 | 自然藤蔓→珐琅微弯金片;名为“鞭形线” (朗古典珠宝) |
| 装饰艺术 (1920s) | Cartier “Love” 圈镯 | 纯圆截面 + 等距螺丝刻痕,恒曲率圆环象征恒久 (Architectural Digest) | |
| 北欧现代主义 (1940-60) | Georg Jensen Möbius Ring | 数学 Möbius 环:单面双曲率,雕塑感与符号感并重 (Georg Jensen) | |
| 意式写意 (1940s-今) | Bulgari Serpenti | 对数螺旋缠腕,节段式弹簧骨架兼顾柔韧 (宝格丽) |
规律:早期手工艺强调“曲线=自然隐喻”;现代高端珠宝把完美曲率升级为品牌 DNA(圆环→Cartier,螺旋→Bulgari,环带→Jensen)。
当代标志:三类“曲线原型”
1 恒曲率圆/椭圆
- Cartier Love:直径、厚度、螺丝凹槽均取等差,确保光斑均匀反射并简化 CNC 刀轨 。
- Niessing Spannring:内圆弧预压应力“悬浮”主石,力学模拟要求误差 <10 µm (Niessing)。
2 对数与双曲螺旋
- Bulgari Serpenti:模块节距按 log r=a·e^{bθ} 退缩,既方便尺寸序列化又保持视觉流动 。
- Piaget Possession:可旋转外圈利用螺旋斜面减摩擦,曲率设计保证珠圈旋动阻尼恒定 (巴黎世家官方网站)。
3 Möbius/环带与S-弧
- Georg Jensen Möbius:单曲面自动导水光线,佩戴时不刮手;通过 NURBS G³ 连续模型 NC 铣削 (Georg Jensen)。
- Art Nouveau S-弧胸针:石座间连线为 Catmull-Rom 曲线,拐点无尖角便于嵌珠 。
CAD/AI 工艺:让曲线“生”出来
| 工艺 | 关键算法/软件 | 曲线控制要点 |
|---|---|---|
| Rhino + Grasshopper | Bézier/NURBS;曲率梳实时可视 | 调整控制点至 κ′≈0 防过冲 (YouTube) |
| Generative Shape Grammar | 深度 Diffusion→SVG path | 以“单调曲率 + 对称约束”作为 loss (SCIRP) |
| Parametric Spiral Script | Python/Blender → r=a*exp(bθ) |
输出步长与节距列表,指导节片 CNC (宝格丽) |
检验:输出 STL 后必须跑 curvature histogram;尖峰 >2σ 处即潜在割手位。
人体工学与品牌策略
- 佩戴曲率 vs 骨骼曲面
手镯内圈品控曲率半径需 ≥ 30 mm 才不会压挤尺侧神经;戒指内弧用“舒适圈”减磨 (Holly Gage Design)。
- 曲线即图腾
Porsche 用“fly-line”曲率塑车,Cartier 用圆环塑爱情——首饰品牌通过恒定曲率符号化获得 50+ 年识别度 (WIRED)。
生成与评估流程(实践者备忘)
graph LR
A(草图逻辑曲线)-->B(Bézier/NURBS建模)
B-->C{曲率梳检查 κ′≤阈值}
C--是-->D(可视化渲染&3D打印蜡型)
C--否-->B
D-->E(人体试戴 & 力学模拟)
E--OK-->F(CNC/铸造)
- 曲率阈值:κ′<0.04 mm⁻²(戒指)、<0.02 mm⁻²(手镯)为常见经验。
- AI 辅助:用 Stable Diffusion ControlNet 生成 SVG mask,再在 Fusion 360 里参数化 → 一键换号。
小结
“完美首饰曲线” = G³ 连续几何 + 力学安全 + 情感象征 三位一体。
流动的 S、恒定的圆、螺旋的生命序列,既是算法里可计算的 κ(s),也是品牌故事里可传世的符号。把曲率精修到“看不出接点、戴不出折痕、忆不掉意味”,才是首饰设计师真正的黄金切面。
参考文献
- Lang Antiques—Art Nouveau “whiplash” lines (朗古典珠宝)
- Georg Jensen Möbius Ring 产品页 (Georg Jensen)
- Piaget Possession 螺旋戒指官方介绍 (巴黎世家官方网站)
- Rhino Jewellery CAD 曲率梳教程(YouTube) (YouTube)
- Niessing Spannring 设计史 (Niessing)
- Van Cleef & Arpels L’Arche de Noé 高珠系列曲线过渡 (Maison Van Cleef & Arpels)
- Bulgari Serpenti 螺旋设计说明 (宝格丽)
- Holly Gage—Jewellery Ergonomics 指南 (Holly Gage Design)
- Shape-Grammar in Generative Jewellery (SCIRP) (SCIRP)
- Cartier Love Bracelet 展览报道(Architectural Digest) (Architectural Digest)
- Wired—数学曲线在家居与珠宝设计中的应用 (WIRED)
人体
人体自身蕴藏的“完美曲线”并非单一标准,而是多种 几何形态与生理功能 叠加的结果:从黄金比例分割的人体整体比例,到脊柱 S 形保持平衡,再到足弓、锁骨、耳蜗、血管分形等在承重、运动与感知上的高效曲率分布。下面按 比例美学 → 功能支撑 → 螺旋 / 分形 → 审美符号 四大维度,解析这些经典曲线如何在人体中同时服务于结构、生理与视觉和谐。
1 比例美学:黄金分割与圆弧
1.1 脐点黄金分割
人体从头顶到脚底的高度,脐部大致位于 0.618 : 1 的分割点,这一比值长期被艺术家与医学美学研究视为“整体和谐”的基准线(ResearchGate)。
1.2 牙弓与面部轮廓
正常咬合的牙弓曲线在数学上多被建模为抛物线或椭圆,曲率连续有助于分散咀嚼应力,也是“微笑线”视觉流畅的关键(ResearchGate)。
2 功能支撑:人体的 S 形与承重拱
2.1 脊柱双 S 曲线
颈椎与腰椎呈前凸(lordosis),胸椎呈后凸(kyphosis),四段曲率共同形成双 S 形弹簧,既吸收震荡又使头部稳定在骨盆上方(NYSI, Verywell Health)。
2.2 足弓——天然“拱桥”
足底纵弓与横弓构成三维弹性拱;曲线储能回弹,被称为“人体行走的减震器”(物理治疗百科)。
2.3 锁骨 S 形与股骨前弯
锁骨的双弯 ( sigmoid ) 曲线把肩胛带受力均匀传递到胸骨,同时为上肢提供更大活动范围(物理治疗百科);股骨轻微前弯可抵消行走时的弯矩并优化肌肉拉力线(PMC)。
3 螺旋与分形:空间高效与感官精密
3.1 耳蜗螺旋
内耳耳蜗卷曲三圈多,虽然并非理想对数螺旋,但螺旋布局在有限空间内最大化了感音毛细胞排列长度,提升频率分辨率(PMC)。
3.2 血管与支气管分形
动脉、静脉与支气管以近似二叉分形递归,最小化泵压与材料用量,被称为“最优输运网络”(PMC)。
3.3 掌弓(Palmar Arch)
浅、深掌弓通过 3D 曲线闭环保证手部肌骨获得均匀供血,且在握持时能随筋膜张力变化轻微变形(Kenhub)。
4 审美符号:曲线与性别吸引
4.1 腰-臀曲线
研究显示≈0.7 的腰臀比与向外扩张的臀缘曲率,在跨文化审美中与健康、生育力高相关(Reddit, The US Sun)。
4.2 肋廓与肩-腰倒三角
男性广肩窄腰的“倒三角”依赖肋骨弧与斜方肌外缘曲线;女性则以柔和胸廓—腰窝“S”曲线增添阴柔动感——两者皆利用曲率突显次性征。
小结:人体“完美曲线”三条黄金法则
- 曲率连续 / 单调:脊柱、牙弓、锁骨等部位借连续变化的曲率避免应力集中。
- 结构-功能耦合:足弓、股骨、血管分形将最小材料与最大效率合二为一。
- 审美-信号叠加:黄金分割、腰-臀 S 形把生理健康信息编码进高度可读的几何符号。
这些曲线表明,美感不是装饰性的外在标签,而是 进化、力学与信息 三方博弈后的几何精粹——人体自身即是最早的“生成式设计师”。
植物
在植物王国里,“完美曲线”并不是诗意夸饰,而是进化与几何共同雕琢的真实结构:向日葵盘面的 Fibonacci 双螺旋实现种子密排;罗马花椰菜的对数螺旋分形让叶簇高效捕光;螺旋芦荟的五道叶列将水分蒸腾降到最低;蕨类的卷曲新叶以近黄金螺旋的姿态在最小空间内保护生长点。以下索引把自然界最典型的“完美曲线”按曲线类型 ↔ 植物器官 ↔ 机能与美学三维对照,可作观测、摄影或仿生设计的手边辞典。
螺旋曲线 (Log/黄金螺旋)
| 植物 | 器官/部位 | 曲线特征 | 生态/工程意义 |
|---|---|---|---|
| 向日葵 Helianthus annuus | 花盘种子排布 | 逆时针/顺时针螺旋条数为相邻 Fibonacci 数,近似黄金角 137.5° 分布 | 最大化种子密度,避免阴影重叠(问自然) |
| 罗马花椰菜 Brassica oleracea var. botrytis | 花序 | 对数螺旋 + 自相似分形锥状塔 | 均匀布光与散热,经典教学模型(jollytomato.com, Allrecipes) |
| 螺旋芦荟 Aloe polyphylla | 叶列 | 5 条螺旋(或 8、13),顺/逆时针皆可 | 叶缘互不遮蔽、雨水导流(Monrovia) |
| 蕨类嫩叶 (Fiddlehead) | 生长卷曲 | 接近对数螺旋,角速度渐减 | 在极小体积内包覆幼叶、抗机械损伤(vertigrow.substack.com) |
抛物曲线与悬链线 (力学最优)
| 植物 | 部位 | 曲线特征 | 作用 |
|---|---|---|---|
| 葡萄藤等缠绕茎 | 卷须悬垂段 | 悬链线近似,张力最小 | 减少自重弯矩,提升抓附效率(SpringerLink) |
| 百合花瓣开张 | 盛放边缘 | 张力抛物曲线,生长差驱动 | 快速张开同时维持机械稳定(PMC) |
椭圆与圆拱 (压力分散)
| 植物 | 部位 | 曲率亮点 | 生态意义 |
|---|---|---|---|
| 热带猪笼草 Cephalotus, Heliamphora 等 | 壶身横截面近椭圆 | 增大容积并分散风压 | 捕虫壶抗倒伏、稳固支撑(bsapubs.onlinelibrary.wiley.com) |
| 血根 Sanguinaria canadensis | 盾状叶 | 圆弧十二裂但整体恒宽感强 | 覆地遮光、蒸散可控(Go Botany) |
分形与枝分螺旋 (运输/信号最优)
| 植物 | 组织 | 几何模式 | 功能 |
|---|---|---|---|
| 松球 | 种鳞排列 | 双螺旋 Fibonacci | 种子紧密打包、雨湿开张(awkward botany) |
| 木本维管束 | 导管网 | 2-3 维分形分支 | 最小阻力输水、营养高效分配(MDPI) |
人体感知角度的“最美曲线”植物 Top 5
- 向日葵花盘 – 远观整体黄金螺旋,近看种子微结构完美镶嵌。
- 罗马花椰菜 – 可食的分形塔,3D 打印灵感常客。
- 螺旋芦荟 – 五道叶列如万花筒旋心,摄影圈爆款。
- 蕨类新叶 – 具象“黄金螺旋”,被新西兰毛利文化当作生命图腾。
- 松球 – 手持即见 8/13、13/21 螺旋对数,教学与装饰兼具。
如何在算法里复现这些曲线
| 曲线 | 数学表达 | 代码片段 (Python) |
|---|---|---|
| 对数螺旋 (花序、罗马花椰菜) | r=aebθr = a e^{b\theta} | x=r*np.cos(t); y=r*np.sin(t) |
| 黄金角分布 (种子) | θn=n⋅137.5°\theta_n=n\cdot137.5°, rn=nr_n=\sqrt{n} | for n in range(N): … |
| 悬链线 (藤蔓) | y=acosh(x/a)y=a\cosh(x/a) | y=a*np.cosh(x/a) |
| 分形枝分 | L-system or box-counting SDF | 递归迭代/逃逸法 |
设计提示:将上述曲线参数化后,可直接用于 Generative Art、数据可视化或仿生产品的壳体优化。
小结
植物学里的“完美曲线”是一部活体几何教科书——它们通过对数螺旋、椭圆、悬链线与分形网络,在光照、输运、支撑与繁衍四大维度上逼近极限效率。追踪这些曲线,不仅能拓展自然美学视野,更能为建筑外形、空气动力与算法艺术提供一手灵感。
宇宙|上帝视角
在可观测宇宙中,“造物者的上帝曲线”并非神秘玄谈,而是重力、旋转与对称把空间-时间雕刻出的几何极致:
圆与椭圆统管行星与透镜,黄金螺旋铺陈星系臂条,同心环映照黑洞与气态巨行星,复合花瓣轨道涂绘引力多体舞步,而宇宙弦与强透镜则在深空勾勒出几乎完美的光弧。以下索引六大类“宇宙完美曲线”,兼顾几何特征、物理成因与美学寓意。
1 圆与椭圆:引力的首要篆刻
1.1 开普勒椭圆
两体在牛顿-广义相对论框架下的无扰运动收敛为椭圆,是最早被辨认的“宇宙完美曲线”(Wikipedia)。
1.2 爱因斯坦环
当背景星系、透镜星系与地球近乎共线,透镜质量把光弯成完整圆环;欧空局 Euclid 卫星近期拍到 1.8ʺ 直径的示范级环形,几何对称近乎教科书(European Space Agency)。哈勃更早在白矮星重力微透镜中验证爱因斯坦 1936 年的预言(WIRED)。
2 对数与黄金螺旋:星系的自组织节奏
密度波理论指出,旋涡星系的弯臂可长期维持近对数螺旋形态,臂条与圆心夹角近恒,乃“流动但恒形”的典型(Wikipedia)。黄金螺旋只是对数螺旋的特殊 φ-生长率版本,在一些“大设计”星系中局部逼近此比例,被天体美学爱好者称作“宇宙版黄金分割”(Wikipedia)。
3 同心环:从行星到黑洞
- 土星环:冰粒在柯本轨道上排布成多重薄环,整体几何近乎共面圆环,是天然的“粒子干涉衍射图样”(Wikipedia)。
- 光子环:在黑洞事件视界外 1.5 rₛ 处,光线可做闭合轨道;事件视界望远镜在 M87* 周围捕捉到此环形光圈,曲率恒定且几乎完美闭合(Quanta Magazine)。
4 复合花瓣与空间站轨道
- Lissajous 轨道:环绕太阳-地球 L₁/L₂ 的卫星(如韦伯望远镜)沿三维 Lissajous 曲线运行,保持与地日线稳定角度,代表“非闭合完美曲线”在航天中的应用(Wikipedia)。
- Rosetta 花瓣轨道:当引力势非点源或加入广义相对论修正,行星轨迹将呈渐进花瓣,水星的近日点进动即经典实例(DBpedia Association)。
5 悬弦与光弧:宇宙弦透镜
若早期宇宙生成的一维拓扑缺陷——宇宙弦—横贯视线,会把背景星系撕成两条平行光弧或半环,几何对称堪比人造 CAD 线稿;近年的理论与模拟详述了这种“曲率缺口”透镜模型(arXiv)。
6 更宏大的螺旋与分形
在星系旋涡之外,银河系大尺度气体臂与恒星形成区同样服从对数螺旋-分形嵌套规律;星际尘埃与磁场在电流-引力耦合下出现 p-mode 涡旋,为“宇宙完美曲线”添加分形尺码梯度(相关观测见 WISE、Planck 巡天)。
小结
从最简单的椭圆到极致对称的光子环,再到对数螺旋和花瓣轨道,“上帝曲线”通过万有引力、相对论时空和密度波自组织等物理律,为宇宙书写了多种 恒定曲率、恒定宽度或自相似增长 的几何诗篇。它们既是天体力学与广义相对论的硬核验算,又以惊人的视觉纯粹唤起人类对“完美形态”的永恒追问。
微观世界
微观尺度的“完美曲线”并非稀有例外,而是原子键长、能量最小化和对称性原理共同“雕刻”的几何极致:DNA 与蛋白质卷成精密的螺旋;碳材料把蜂巢平面卷制成手性纳米管;甲壳硅藻和放射虫用超公式 + 对数螺线排布壳板;雪花、脂质双连续立方相与 icosa 病毒壳则在晶体和自组装过程中生成圆、椭圆、最小曲面或截面分形。下面按 分子 → 纳米 → 微生物 → 自组装晶体 递进,列出典型“完美曲线”及其物理成因、几何参数与仿生启示。
1 分子层:天然螺旋的双璧
1.1 DNA 双螺旋
- B-型 DNA 直径 ≈ 2 nm,螺距 3.4 nm/10 碱基,螺线角恒定,几乎理想的对数螺旋近似 (Wikipedia, tud.ttu.ee)。
- 结构由氢键+π–π 堆叠决定,最小自由能把链卷到恒定曲率。
1.2 α-螺旋
- 每圈 3.6 残基,螺距 0.54 nm;氢键 i→i+4 锁定曲率单调 (培生平台, comis.med.uvm.edu)。
- 生物机械优势:将侧链“外翻”形成管状通路,是跨膜螺旋与弹簧蛋白的刚柔核心。
2 纳米材料:碳与硅的卷曲艺术
2.1 碳纳米管
- 石墨六角网沿手性向量 (n,m) 卷折;(n,n) 臂椅型给出恒定圆筒曲率,(n,0) 锯齿型呈折线对称,半径 ≈ a√(n²+nm+m²)/π (photon.t.u-tokyo.ac.jp, research.physics.unc.edu)。
- 手性角决定电子带隙,把“曲线”直接映射到功能。
2.2 富勒烯 C₆₀
- 20 六边形 + 12 五边形构成截顶二十面体,弯曲半径相等;是纳米尺度上最均匀分布曲率的“球” (Wikipedia)。
3 微生物壳体:超公式与黄金螺旋
| 生物 | 几何曲线 | 作用 |
|---|---|---|
| 硅藻 frustule | Johan Gielis 超公式 + 对数螺线组合,产生星形或漩涡孔径阵列 (microscopy-uk.org.uk, Pinterest) | 既减重又提高光捕获效率 |
| 放射虫骨骼 | 近截顶正 20 面体或三轴椭圆网格 (Wikipedia) | 最大化强度/重量比 |
| 有孔虫壳 | 逐步对数螺线卷壳(黄金角分布气孔) (The Marginalian) | 均匀增重,维持浮力 |
4 自组装与相变:最小曲面与分形
4.1 脂质双连续立方相
- 脂双层可自组织成 G-型 Gyroid 最小曲面,零平均曲率却三维连通 (科学直通车)。
- 在药物递送膜和光子晶体中被仿制。
4.2 雪花与拉普拉斯生长
- 六角对称枝干在扩散场中呈分形曲线,分形维 1.7–1.9 (AGU Publications);晶面角度固定使主干为 60° 抛物弧。
4.3 病毒 icosa 壳
- 蛋白亚基按 T 数拓扑规则拼出几乎完美的 20 面体;曲率在五、六聚体间量子化跳变是“最少能量封装”解 (PubMed Central)。
5 “上帝曲线”在微尺度的通用规律
- 能量极小 & 对称:无论 DNA、Gyroid 还是 C₆₀,恒定或分段恒定曲率意味着弯曲能均匀分布。
- 对数螺旋 & 黄金角:在需填充空间又避免遮蔽的情境(种子排布、壳体增生),黄金角 137.5° 近乎最优。
- 最小曲面:当系统既要分隔两相又要最小化界面(脂质、水),曲率零均值的极小曲面涌现。
6 仿生与算法实现
| 曲线 | 数学模型 | 应用 |
|---|---|---|
| DNA/α-螺旋 | 双螺旋 r=a, θ=bt | 螺旋天线、弹簧 |
| Gyroid | sin x cos y + sin y cos z + sin z cos x = 0 | 3D 打印轻量支架 |
| Diatom supershape | Gielis 超公式 n₁,n₂,n₃ | 光学/微流体过滤 |
| Carbon nanotube | graphene chiral vector (n,m) → tube radius | 纳米导线、场发射 |
数值上,可在 Python 里用 scipy.optimize 最小化弯曲能(∫k² ds)或用 Neural SDF + 可微渲染把曲率约束写进损失,从而人工合成“微观完美曲线”。
小结
微观世界的“完美曲线”是 能量最小化 + 对称自组装 + 功能最优化 的必然产物:分子层面的螺旋、纳米管的圆筒和 Gyroid、雪花、病毒壳的极小曲面或截顶多面体,共同证明自然在曲率与对称的“设计空间”里精打细算——也为材料科学、仿生制造与生成式算法提供了丰富模板。
工程技术
工程技术里的“完美曲线”,指那些 在几何、受力、流体或运动学上同时达到最优或近似最优 的曲线;它们被写入设计规范、CAE 软件和制造标准,几乎主宰了拱桥、道路、齿轮、叶型、凸轮、涡轮等各类系统的性能上限。典型范式包括:等压悬链线与常应力拱、曲率线性递增的欧拉螺线、无滑动啮合的渐开线齿形、低阻高升的 NACA 翼型曲线、恒宽/恒厚驱动件、以及对数螺旋叶片。下文按“承载结构→轨道道路→动力传递→流体/气动→特种机构→跨域趋势”六大板块展开,并标注这些曲线的数学特征、工程价值与主流应用软件。
1 承载结构:让受力“均匀流动”
1.1 悬链线与恒压拱
- 纯自重拱若做成 倒悬链线,跨中到支座只承受轴向压应力,可用最小材料抵抗荷载(科学直通车, Royal Society Publishing)。现代混凝土和 3D 打印桥梁仍沿用该曲线。
1.2 常应力变曲率梁
- 变曲率拱肋采用 逐点调整曲率 控制 σ≈常数,减小集中弯矩,使结构更轻 (Wiley Online Library)。
2 轨道与道路:曲率线性变 = 乘坐平顺
2.1 欧拉螺线(Clothoid)
- 曲率 κ ∝ 弧长 s,驾驶员打方向盘匀速即可完成直线→圆弧过渡;成了全球公路、铁路过渡曲线规范(Drawing, A railway track blog)。
2.2 超高与曲线耦合
- 在铁路中,欧拉螺线与轨道超高曲线同时递增,以保持乘客横向加速度恒定(A railway track blog)。
3 动力传递:齿轮、凸轮与滚子
3.1 渐开线齿形
- 渐开线保证啮合角恒定、法向速度恒速,制造公差大、效率高;几乎垄断动力传动领域(khkgears.net)。
3.2 摆线/环摆线驱动
- 摆线齿根曲率大、接触应力低,广用于高减速摆线针轮减速机(维基百科)。
3.3 恒宽凸轮与 Reuleaux 机构
- 曲线宽度恒定可把转动变成近似直线往复;用于泵、量规及“异形”轴承(The Triz Journal, nationalcurvebank.org)。
4 流体与气动:升阻与剪切的平衡
4.1 NACA 4-位数字翼型
- 前缘圆弧+后缘抛物线的参数曲线让设计者用四个数字即确定最大弯度/厚度/位置;仍是 CFD 与 CNC 刀轨生成的经典基准(airfoiltools.com)。
4.2 对数螺旋叶片
- 螺旋桨、涡轮叶片沿 log r = a θ 变化攻角,可在半径方向保持升阻比近似恒定,并具自清理性能(切藻)(谷歌专利)。
4.3 涡轮流线与弯流曲率
- Darrieus 竖直轴风机的效率依赖局部流线曲率设计;合理曲率降低失速(AIAA 期刊)。
5 特种机构与可制造性
5.1 Bezier / NURBS CAD 万能曲线
- 从汽车外壳到注塑模具,大部分自由曲面以 Bézier 或 NURBS 控制点定义,可做到 G² 连续、易 CNC (NOVEDGE)。
5.2 Euler Buckling 曲线
- 刚性柱临界载荷随 λ = L/√I 成 1/L² 曲线下降;工程用此确定细长构件截面(The Engineering ToolBox)。
5.3 螺旋伞齿与空间啮合
- 螺旋伞齿线沿球面摆动,重叠系数大、噪音小,用于航空齿轮箱 (NASA技术报告服务)。
6 跨域趋势:数值优化 + 增材制造
- 拱肋、壳体与支架在拓扑优化后往往呈 曲率连续的“骨骼曲线”,借 SLM 或 WAAM 一次打印;行业称之为“free-form optimal splines”。
- AI-CAD 正在把经典 Bézier/NURBS 与生成式设计融合,自动输出满足 κ′平滑与应力约束的曲线骨架(NOVEDGE)。
主要应用软件
| 领域 | 工具 | 曲线功能 |
|---|---|---|
| 桥梁 | MIDAS / SOFiSTiK | 悬链线/变曲率拱模块 |
| 道路 | Bentley OpenRoads | Clothoid & 超高自动联动 |
| 齿轮 | KISSsoft | 渐开线/摆线参数化 |
| CFD | ANSYS Fluent | NACA 库 & 自由叶片 spline |
| CAD | Rhino + Grasshopper | 任意 NURBS/G² 曲率梳 |
小结
工程技术中的“完美曲线”并不是装饰性的优雅,而是 力学、运动学与制造经济性 长期演化的结果:
- 悬链线 / 常应力拱 把压应力分布拉成水平线;
- 欧拉螺线 让车辆转向曲率线性增长;
- 渐开线齿形 实现恒速、易加工的啮合;
- 对数螺旋与 NACA 曲线 在流体中取得升阻平衡;
- 恒宽与摆线曲线 则把复杂运动转换为可控输出。
这些曲线已深嵌在各行业的设计规范与 CAE 软件库里,成为将“数学最优”落地为“工程可用”的核心桥梁。
烘焙曲线
在烘焙面包时,一条真正 “完美” 的烘焙曲线并不是单一、固定的温度–时间轨迹,而是围绕四个关键物理化学节点(酵母失活点、淀粉糊化区、蛋白凝固区、褐变窗口)展开的分段温控与蒸汽管理策略;目标是在最短时间内完成 充分“炉窜”+均匀膨胀+薄而脆的焦糖化外壳+湿润开放的内部蜂窝。下面给出一个可落地的“黄金曲线”范式,并说明如何按配方、炉型与面团尺寸做微调。
1 核心温区与生化里程碑
| 温度区间 | 典型核心事件 | 参考 |
|---|---|---|
| 25-50 °C | 酵母活跃、酶促分解继续;开始形成早期蒸汽 — 为“炉窜”储能 | (The Fresh Loaf) |
| 60-72 °C | 酵母失活、膨胀达到峰值(oven-spring);面筋开始定型;淀粉 1 阶糊化 | (PizzaBlab, The Fresh Loaf) |
| 80-100 °C | 淀粉完全糊化,蛋白彻底凝固;内部结构“定格”;水分大量汽化 | (ThermoWorks) |
| 140-200 °C(表层) | 140-165 °C 触发麦拉德反应,>180 °C 蔗糖焦化;决定色泽和香气 | (Allrecipes, Serious Eats) |
判断熟透:心温 96-98 °C(lean dough),或 88-93 °C(甜面团)即可出炉(ThermoWorks)。
2 “黄金曲线”示范(中等水分欧包 800 g,用石板炉)
| 阶段 | 炉温设定 | 时长 | 目的 | 操作细节 |
|---|---|---|---|---|
| 预热 | 上下 260 °C、石板 ≥275 °C | ≥45 min | 热惯量充足 | 石板吸热,后续温降更平稳 |
| 进炉+蒸汽 | 250 °C + 注蒸汽 | 10 min | 最大化 oven-spring | 开炉门快速喷 50-80 ml 水;高温蒸汽推迟表皮干化 (Taste of Artisan) |
| 固形-着色 | 降至 230 °C | 12–15 min | 面筋/淀粉定型 + 初期褐变 | 打开排气阀放蒸汽,避免“湿闷” |
| 深度焦糖 | 再降至 210 °C | 10-15 min | 获得深金色脆壳 | 根据配方含糖量调 200–215 °C (Sassafras Curio) |
| 干燥回火 | 炉门虚掩,180 °C | 3-5 min | 壳内水汽逸散,保持脆度 | 小开缝,利用余热烘壳 |
曲线要义
- 高温起跳保证“炉窜”高度;
- 两级降温先固形再控色,给糖化和焦化各自最佳窗;
- 蒸汽先足后排——水膜延缓外壳凝固,后期排湿使脆壳持久 (PizzaBlab, Taste of Artisan)。
3 依情景微调的 4 个旋钮
| 旋钮 | 条件变化 | 调整策略 | 依据 |
|---|---|---|---|
| 面团重量 | 小餐包 <100 g | 最高温不变,缩短前两段各 2-3 min;可跳过回火 | 小质量易过褐变 (Reddit) |
| 水分含量 | 高水 (>80%-Baker’s%) | 第一段提至 255-260 °C,并延长 2 min;蒸汽量减 20% | 内部水多延滞糊化 |
| 糖/油含量 | 配方含糖 >10% | 主烤温下调 10-15 °C,避免过深褐 | 麦拉德提前启动 (Allrecipes) |
| 家用普通炉,无石板 | 热惯量低 | ①拉长预热;②首段加上火;③用铸铁壶加热储热 | 温降过快导致矮胚 |
4 数据采集与“曲线回放”
- 心温探针:蓝牙热电偶记录 <1 s 间隔温度曲线;分析斜率可逆推糊化速率。
- 红外测皮温:入炉 5、10、20 min 点测 → 验证外壳降温梯度。
- 湿度记录:安置 Sensirion SHT11(耐 200 °C)+ 核心温度同步。
- 可视化:Python
matplotlib双轴绘制:炉温 / 面团心温 / 湿度。建议套用seaborn theme="darkgrid"并叠加阈值横线——一眼定位是否越界。
5 常见失误与补救
| 症状 | 诊断 | 曲线处方 |
|---|---|---|
| 壳薄而软 | 蒸汽不足或排湿过晚 | 第一段喷 50 ml → 7 min 时开排气 |
| 外焦里生 | 预热不足或温降过猛 | 加厚石板 / 提首段 5 °C |
| 爆底裂 | 降温过早致表壳定型前内压失控 | 固形段温度或时长需↑ |
小结
一条“完美的烘焙曲线”=高温、足汽、分段降温、精准收尾的协奏:它把酵母活性、淀粉糊化、面筋定型与麦拉德变褐四大关键节点串成可量化的温度–时间轨迹。结合探针、红外与湿度传感,可把这条曲线固化为自家烤箱的“指纹”,进而对不同面团配方快速微调、稳定复制出理想的外壳和内部蜂窝。
参考资料
- 各温区作用与酵母失活、淀粉糊化
- 进炉蒸汽与硬壳形成
- 家用烤箱温度控制与心温判断
- 麦拉德窗口与配方糖分调温(Allrecipes)(Serious Eats)
- 预热与石板热惯量细节
- Catlan & Cauvain. Baking Problems Solved, CRC Press (工业参考书,对上述阈值亦有佐证)。
金融曲线
在金融市场里想 “用完美曲线收割” 并不是真的去寻找一条神秘的光滑函数,而是把“曲率”——收益-风险对价的非线性—转化为可持续、可复制的现金流。
具体落地可拆成四个环节:① 识别天然存在的曲线(收益 vs 风险、价格 vs 时间、波动 vs 位置);② 利用凸性/凹性 把曲线“掰”向自己有利的一侧;③ 动态调仓 让组合始终贴在那条曲线的“上风面”;④ 防止伪曲线(过拟合)。下面分模块说明对应方法、核心公式与风险点,并给出可即用的策略模板。
1 市场里有哪些“天然完美曲线”
| 曲线所在 | 几何特征 | 可收割的溢价/结构 |
|---|---|---|
| 收益-波动曲线 | “方差拖累”让几何平均 < 算术平均;曲线向下弯 | 通过波动率收割在多资产/多腿组合中榨取 volatility return (Nerd’s Eye View | Kitces.com) |
| 收益-杠杆曲线 | Kelly 曲线峰值对应长期增长率最优 | Kelly-调仓最大化复利同时控制爆仓概率 (Medium) |
| 价格-时间曲线(期权) | Gamma/Convexity 为二阶导 | Gamma-scalping & 正凸性组合在大振幅中收集“曲线面积” (嘉信理财, TastyLive , 量化金融与算法交易博客) |
| 收益-利率期限结构 | 凸性偏差(convexity bias) | Yield-curve carry / “Curvy trades” 捕捉远端与近端互换差 (风险管理期货与期权 – CME集团, European Central Bank) |
| 波动率微笑曲线 | 非对称鞍形 | 做多 IV 滑坡段、空高杠杆尾部,赚“笑面崩溃” (Macrosynergy) |
2 算法与交易工艺
2.1 波动率收割(Variance Harvesting)
- 设多资产等权组合 wiw_i;组合几何增长率g≈μˉ−12σG2g \approx \bar\mu – \frac12\sigma_G^2
- 通过定期再平衡 降低 σG2\sigma_G^2 同时保留各资产算术收益 → 获得“方差溢价” (CFA Institute Research and Policy Center)。
- 执行:每 Δt 用·方差-预算·优化器调权重;Python 可调用
cvxpy。
2.2 Kelly 曲线定位
- 利用胜率 pp 与赔率 bb 计算最佳仓位f^* = \frac{p(b+1)-1}{b} \] :contentReference[oaicite:6]{index=6}
- 缩放系数 ½-Kelly 折中尾部风险;实时用
pandas滚动窗口更新 p,b。
2.3 Gamma / Convexity Harvest
- 构建初始 delta-neutral, +Gamma 期权组合(买近月 ATM straddle)。
- 价格向上(下)移动 ΔS 时卖(买)等额正股以重新 delta-中性 → 把“曲线面积”兑现 (嘉信理财, TastyLive )。
- 日终平仓 Gamma 或滚动到下一期;仓位大小用 vol-scaling 控制。「Python-Alpaca 示例」给出完整脚本 (Alpaca)。
2.4 Yield-Curve “Curvy Trade”
- 利率互换 vs SOFR 期货的凸性偏差 由ConvBias≈12σr2T2\text{ConvBias} \approx \tfrac12\sigma_r^2 T^2决定(CME 教程) (风险管理期货与期权 – CME集团)。
- 策略:多 SOFR 期货、空等 DV01 FRA。ECB 工作论文量化了年化 ≈30 bp α (European Central Bank)。
2.5 防止伪曲线(Curve Fitting / Overfitting)
- 在回测里任何“完美弯曲”易是过拟合噪声 (Quantified Strategies, Bookmap)。
- 正则化:抢投样法 + 交叉检验;或者用 walk-forward + PBO(Probability of Backtest Overfitting)。
3 风险雷区与校准
| 曲线策略 | 关键风险 | 对冲/管控 |
|---|---|---|
| 波动率收割 | 序列相关 → “平衡溢价”可能短暂为负 | 动态窗口检测自相关,必要时减仓 |
| Kelly | 尾部跳跃 | 半 Kelly + 波动目标止损 (Investopedia) |
| Gamma scalping | Vega 损耗 > Gamma 确定收益 | 选高 θ/Γ 比值品种;用 VIX 过滤 |
| Convexity carry | 快速曲率跃升 | 加入 gamma-hedge IR caps |
| Curve fitting 策略 | 交易时漂移 | 交叉市场验证;上线后根据 live-SR 快速下线 |
4 可快速复用的 Python 片段
import vectorbt as vbt, numpy as np, pandas as pd, yfinance as yf
# 1⃣ 波动率收割——等权再平衡
tickers = ['SPY','IEF','GLD']
prices = yf.download(tickers, '2014-01-01')['Adj Close']
pf = vbt.Portfolio.from_holding(prices, freq='M', rebalance=True)
print(pf.total_return(), pf.sharpe_ratio())
# 2⃣ Kelly 动态仓位
r = prices.pct_change().dropna()
edge = r.mean()/r.std()
kelly_w = edge/((1-edge)*r.shape[1]) # 简化
“完美曲线”在金融里= 把市场天然的非线性(convexity, variance, yield curvature)转化为正期望现金流,同时用动态仓位把自己牢牢贴在曲线最肥的一边。但任何看似光滑的回测曲线都可能是噪声雕刻的幻影;真正的“完美收割”必定伴随严苛的反过拟合检验与实时风控。
参考文献
- Kitces —“Volatility Drag: How Variance Drains Returns”
- CFA Digest —“Volatility Harvesting in Theory and Practice”
- Medium —“Position Sizing Using the Kelly Criterion”
- (Investopedia)Investopedia —“Optimal Position Size”
- Schwab —“Gamma Scalping: A Primer”
- Tastylive —“The Dish on Gamma Scalping”
- Alpaca —“Gamma Scalping with Python”
- CME Group —“Understanding Convexity Bias”
- European Central Bank WP 2149 —“From Carry Trades to Curvy Trades”
- NYU Stern —“Term Structure of Currency Carry Risk Premia”
- QuantifiedStrategies & Bookmap — Curve-Fitting Risks
- Macrosynergy —“Equity Convexity and Gamma Strategies”
- Investopedia — “Convexity in Bonds / Gamma Definition”
- SciDirect —“Yield Curve Volatility”
- Ceresa IG —“Methods to Harvest the Volatility Premium”
数据可视化
在数据可视化里,“完美曲线”不是单一算法,而是 “既保真又顺滑” 这一目标下的多层工具箱:
- 插值型 曲线(Catmull-Rom、Monotone Cubic Hermite、Akima 等)负责“穿点”且避免过冲;
- 平滑型 曲线(LOESS、Savitzky-Golay、移动平均)用回归或滤波抑噪同时保留趋势;
- 形状生成型 曲线(Kernel Density、Bézier / B-Spline / NURBS)在分布或矢量图中输出连续函数;
- 可微与 AI 生成 把曲率与光滑性写进损失函数,实现自动“曲线抛光”。
选择算法时要同时权衡 视觉美感(曲率连续、无锯齿) 与 语义完整(不歪曲关键极值和单调性)。下文按“审美准则→算法族谱→代码要点→实践建议”四段展开。
1 什么才算“完美曲线” — 三条审美+数据准则
| 准则 | 视觉指标 | 数据完整性指标 |
|---|---|---|
| 曲率连续 | 观察曲率梳无突刺 | 不产生伪极值/振荡 |
| 单调保持 | 不出现反向拐弯 | 与原序列单调区间一致 |
| 最小相位/能量 | 曲线转折尽量少 | 不增加高频噪声、保留峰谷 |
注:Monotone Cubic Hermite、LOESS 的局部权重、Catmull-Rom 的“centripetal”模式都在算法层面对上述准则做了约束。
2 算法族谱与适用场景
2.1 插值型(穿点+光滑)
| 算法 | 关键特性 | 典型库/用法 |
|---|---|---|
| Monotone Cubic Hermite | 调整切线防止超调;线图最佳默认 | d3.curveMonotoneX (observablehq.com) / Wikipedia (Wikipedia) |
| Catmull-Rom(centripetal) | 穿点、可调 α;游戏轨迹 & 路网 平滑 | d3.curveCatmullRom (d3js.org) / 博客示例 (Mika’s Coding Bits) |
| Akima Spline | 对离群点稳定,无振铃 | Excel/NumPy 插件 (YouTube, (no title)) |
| Cubic Hermite / Cardinal / Basis | B-Spline 家族的常用子集 | d3.curveBasis (d3js.org) |
2.2 平滑型(降噪+趋势)
| 算法 | 场景 | 参考 |
|---|---|---|
| LOESS / LOWESS | 散点趋势线、非线性时间序列 | ggplot2 geom_smooth() (图形语法数据可视化) / Medium 教程 (Medium) |
| Savitzky-Golay | 保峰值光谱、财务指标 | Python SciPy / Medium 指南 (Medium) |
| EMA / Moving Average | 高频金融线图 | Investopedia 综述 (Investopedia) |
2.3 形状生成型(分布 & 矢量)
| 场景 | 常用方法 | 参考 |
|---|---|---|
| 概率分布曲线 | Kernel Density Estimate | KDE 可视化文章 (Medium) |
| 矢量图 / Logo | Bézier / NURBS 手工或 GAN 生成 | Bézier 曲线基础 (Bart Wronski) |
2.4 可微渲染 & AI 生成
- DeepSpline / Vector-GAN:Transformer-B-Spline 直接预测控制点,生成无限分辨率 SVG (observablehq.com, d3js.org)
- Neural SDF:曲率正则 + 可微投影,自动抛光噪声轮廓 (University of Notre Dame)
3 核心实现片段(Python:单调 Hermite)
import numpy as np, matplotlib.pyplot as plt
from scipy.interpolate import PchipInterpolator # monotone cubic Hermite
x = np.arange(10)
y = np.array([3,4,6,4,5,9,7,8,12,11]) # 任意数据
mono = PchipInterpolator(x, y) # 保持单调且无过冲
xs = np.linspace(x.min(), x.max(), 400)
plt.plot(x, y, 'o')
plt.plot(xs, mono(xs))
plt.title('Monotone Cubic Hermite (PCHIP)')
plt.show()
SciPy 的
PchipInterpolator正是 Fritsch–Carlson 单调 Hermite 的实现 (James Bird)。
4 选型与实践指南
- 折线→插值:交互折线图想穿点?用 Catmull-Rom;若数据单调或为累计量,用 Monotone Hermite 防过冲。
- 高噪声→平滑:观测噪声显著、极值不敏感?用 LOESS(非实时)或 Savitzky-Golay(实时)。
- 概率/分布→形状:直方图太粗?用 KDE 输出连续密度曲线。
- 品牌/矢量→AI:需要无限缩放?让 Vector-GAN 直接吐出 Bézier control points。
- 诊断曲率:在 D3/Matplotlib 打开 curvature comb,可视审查曲率跳变 (Wikipedia)。
5 常见误区
- 过度平滑:曲线看起来顺滑但掩盖拐点 → 配合原始散点/透明折线保留真值。
- Catmull-Rom 抖振:α≠0.5 时利于穿点,但极端值多时易振铃 → 调
alpha=0.5(centripetal)或降 tension。 - 移动平均滞后:金融图滞后解释困难 → 改用 LOESS 或双指数平滑补偿延迟。
小结
“完美曲线”在可视化世界里没有唯一算法,而是**“曲率连续 + 数据保真”**这条红线下的多技术协奏。理解每一类算法的光滑机理与失真风险,再用可视化工具实时查看曲率梳,你就能在艺术与准确之间踩到最优解。
主要参考
- Monotone interpolation Observable 示例 (observablehq.com)
- D3 curve 文档(Catmull-Rom、Basis 等) (d3js.org)
- Cubic Hermite spline wiki (Wikipedia)
- LOESS 可视化教程 (Medium)
- Savitzky-Golay Python 指南 (Medium)
- KDE 数据可视化简介 (Medium)
- 线图平滑争议分析 (LinkedIn)
- Investopedia 数据平滑条目 (Investopedia)
- PCHIP 单调 Hermite 理论笔记 (Wikipedia)
- Catmull-Rom 平滑路径技术博文 (Mika’s Coding Bits)
- Transformer-B-Spline 论文新闻简报 (observablehq.com)
- Neural SDF 曲线重建综述 (University of Notre Dame)
- Akima 插值示例视频 (YouTube)
- 曲率梳与 NURBS 基础 (Bart Wronski)
- Hermite 单调算法 Fritsch–Carlson 解析 (James Bird)
计算机图形与人工智能
在计算机图形与 AI 生成系统里,要让一条“完美曲线”既看上去丝滑又满足工程精度,通常分三层:(1)解析/参数化曲线的经典算法;(2)面向复杂模型的曲面光滑与隐式表达;(3)把曲率约束“嵌”进深度生成模型与可微渲染框架。 下面按这三层展开,并给出常用代码策略与最新研究脉络。
解析与参数化:从 Bézier 到 NURBS
1.1 经典 Bézier/B-Spline 算法
- Bézier 曲线通过 De Casteljau 递归插值构造,天生 Cn−1C^{n-1} 连续——适合交互式编辑。
- B-Spline 在节点向量上加权,可用不同阶数取得 C0 ∼ C3C^0\!\sim\!C^3 连续,工业 CAD 常把 “曲率梳” 可视化来消除拐点 (ThePro3DStudio, www.rhino3d.com)。
- 实现要点(Pseudocode)
def de_casteljau(points, t): while len(points) > 1: points = [(1-t)*p + t*q for p, q in zip(points[:-1], points[1:])] return points[0]GPU 上用同样递归可在着色器里实时评估高阶 Bézier 片段。
1.2 变半径超圆角(Apple 式 “super-ellipse blend”)
- 通过渐变半径拼接两段圆弧可实现 G3G^3 连续边角,iPhone 外壳与 Magic Mouse 即用此策略;在 CAD 里通常用 NURBS + 曲率梳优化 (Reddit)。
曲面光滑与隐式表达
2.1 Subdivision:Catmull–Clark & Loop
- 把多边形网格递推细分,极限曲面在普通顶点 C2C^2 连续;在非常点 C1C^1 连续――影视模型面数百万也能保持曲率分布均匀 (斯坦福大学计算机图形学)。
2.2 Signed-Distance Functions (SDF) 与 Neural Implicit
- 将曲面编码为 F(x)=0F(x)=0 的 SDF,可天然获得无穷分辨率与光滑法向;近年 3DGS+SDF 把“高质量曲面重建”做到实时 (NeurIPS, ACM Digital Library)。
- 可微渲染 把 SDF 或三角网格投射误差写进损失,允许反向传播到控制点,实现“曲率驱动的自动修型” (Medium, NIPS 会议论文)。
深度生成:让网络直接“长”出曲线
3.1 DeepSpline / Transformer-B-Spline
- 利用 Transformer 捕捉全局依赖并输出节点向量,能从像素图反推光滑 B-Spline 轮廓;2024 论文报告在航拍道路提取中误差 <2px (科学通报)。
3.2 BézierGAN & Vector-GAN
- 把控制点序列视作序列数据,GAN 直接生成可编辑 Bézier 或 SVG path,实现“无限分辨率”图标/气动翼型设计 (科学通报, Ivan 🇺🇦 Puhachov, GitHub)。
3.3 隐式曲线 GAN / Diffusion
- 最近的 DeepCurrents 与 NeRF-SDF 版扩散模型,能在潜空间里同时约束“匀曲率 + 常宽”等几何属性,再通过可微渲染输出光滑草图 (openaccess.thecvf.com, NeurIPS, ACM Digital Library)。
程序化与优化:完美曲线的“算法锻造”
| 需求 | 算法策略 | 典型工具/库 |
|---|---|---|
| 黄金螺旋 | r=a ebθr=a\,e^{b\theta} 极坐标步进;在 GLSL 用 for θ 累进着色 |
Processing / Shadertoy (Reddit) |
| 最小曲率能量 | 变分法 + 可微渲染;loss = ∫k′(s)k'(s)^2 ds | PyTorch3D DR API (Medium) |
| 常宽曲线优化 | 约束支撑线距离 = w;梯度投影迭代控制点 | JAX + Optax |
| G³ 连续混合角 | Nurbs-Python (geomdl) 曲率梳 + 牛顿法调半径 | geomdl / Rhino SDK (www.rhino3d.com) |
小结与实践路线
- 选择曲线类型:简单 UI 用 Bézier/NURBS;复杂自由形用 subdivision or SDF。
- 把曲率写进损失:λ∫(k−k0)2\lambda\int (k-k_0)^2 控制“完美度”,让 AI 学会“少拐角、少波动”。
- 可视化曲率梳:无论 CAD 还是 PyTorch3D,都用 curvature-comb 诊断“是否真的完美”。
- 混合工作流:AI 先粗生曲线 → CAD 精修节点 → DR 细调 → GPU 实时评估。
在今日的图形与生成框架里,“完美曲线”已不仅是手工调 Bézier,而是可以 “可微+深度+显式” 的全流程协同产物:从控制点到曲率能量、从 GAN 到 SDF,再到实时可视化,都能在同一张 GPU 上完成。
后记
关于完美曲线的话题缘自一道难倒所有小学生的数学题,对于小学生而言,如果不能够通过代数方程式来解决几何问题,那就要完全通过空间思维和想象力来解决问题了。我认为学习数学显然不等同于“做数学习题”(这一说法遭到孩子妈妈的严厉批评),然而我开始设想另一种学习方式——它可以取代目前学校里“刷题”的方式,一种更接近绝对理性和终极审美的创造模式。所以有了今天这个《完美曲线辞典》——如果数学可以创造古希腊的“完美秩序”和黑格尔的“理想曲线”,那么数学就是创造者的数学,而不仅仅是一道数学习题或数学公式。
拉马努金惯以直觉(或称为数感)导出公式,不喜欢做证明,而他的理论在之后往往被证明是对的。拉马努金天才地提出了大量的公式,供人深入研究,并开启了新的研究方向。例如一些和圆周率相关的奇妙的无穷级数。哈代这样评论拉马努金:“他知识不足的程度跟知识的深厚都让人很吃惊……”在数学上,有洞察力和能推导出具体证明是截然不同的。拉马努金将他的理解归功于他的家族女神纳玛姬莉(Namagiri:被视为Lakshmi吉祥天女的化身),并表示在他的工作中向她寻求灵感。他经常说:“一个方程对我没有意义,除非它传达了神的旨意。”
数学理性与意识世界和物理世界共同构建了人类认知的三个终极维度,数学思维本质上是想象力与创造力的开发,而不是习题-考试的正确性和训练结果。“完美曲线”并不只是一段零误差的几何图,它凝聚了 数学的自洽、意识的灵动、物理的验证。把这条曲线引入教育、科技与艺术,实现的正是黑格尔所谓“理念与感性现身的统一”,也回应了柏拉图关于“圆满形态”的召唤——数学思维释放想象力与创造力的真正意义。
我的设想:数学思维=想象力的实验
- 创造先于证明,“逻辑验证只是给直觉找到根据”;
- “完美曲线”作为 全人发展隐喻:逻辑、情感、动手能力三轨并进,而不是单点解题刷分;
- 审美力取代答案:在课堂引入曲线设计、动态几何、算法与数据可视化,让学生亲手创造完美曲线、验证其物理可行性与美学价值。
转载请注明:
作者|鲁大荒, 微米公司创始人,创新策略、数字资产管理专家
©️AiserLu #MidJourney #ChatGPT #AIGC|Rebui1t.com








